Crossed ladders problem facts for kids

The crossed ladders problem is a clever math puzzle. It has been around for a long time and often appears in puzzle books and online discussions. It's a great way to use geometry and algebra to solve a real-world problem.

The Puzzle

Two ladders crossing in an alley. We know the ladder lengths (a and b) and the crossing height (h). We need to find the alley's width (w).

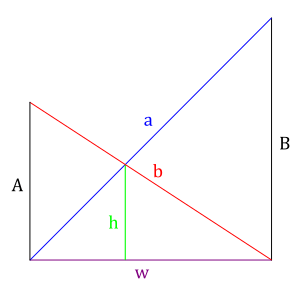
Imagine two ladders leaning across an alley. They stand on opposite sides and cross each other in the middle. You know the length of each ladder. You also know the exact height where the two ladders cross. The big question is: How wide is the alley?

This puzzle seems simple at first. But finding the answer can involve some tricky math! A famous puzzle writer, Martin Gardner, wrote about this problem in 1979. He found that people were talking about it as early as 1895. The puzzle is popular because it looks easy but can quickly become a real brain-teaser.

Solving the Puzzle

To solve the crossed ladders problem, we need to use some geometry. Imagine the ladders, the walls, and the alley floor. They form several right triangles.

One key idea in solving this puzzle is a special relationship between the heights. If we call the height of the wall where ladder b leans A, and the height of the wall where ladder a leans B, then there's a cool rule:

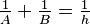
This means that if you take 1 divided by wall height A, and add it to 1 divided by wall height B, you get 1 divided by the crossing height h. This rule is sometimes called the "optic equation."

Why the Optic Equation Works

We can understand this rule by looking at the triangles formed.

• Imagine a small triangle formed by the left wall, the ground, and the part of ladder a up to the crossing point.
• Then imagine a larger triangle formed by the left wall, the ground, and the entire ladder a.
• These two triangles are similar triangles. This means their shapes are the same, even if their sizes are different. Their angles are the same.

Because of similar triangles, we can set up proportions. These proportions help us show that the relationship 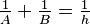is true.

Using the Pythagorean Theorem

Once we know the wall heights (A and B), we can find the alley's width. We use the Pythagorean theorem. This theorem says that in a right triangle, the square of the longest side (the hypotenuse) is equal to the sum of the squares of the other two sides.

• For ladder a: 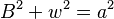Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): B^2 + w^2 = a^2 (where w is the alley width)
• For ladder b: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A^2 + w^2 = b^2

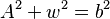
By using these equations along with the optic equation, you can find the value of w, the width of the alley. The full solution involves advanced algebra, often leading to a type of equation called a "quartic equation." This kind of equation can be complex to solve, but it gives us the exact answer for the alley's width.

Whole Number Solutions

Sometimes, all the numbers in the crossed ladders problem can be integers (whole numbers). This means the ladder lengths, wall heights, alley width, and crossing height are all whole numbers.

For example, one such solution is:

• Ladder lengths: a = 119, b = 70
• Wall heights: A = 42, B = 105
• Alley width: w = 56
• Crossing height: h = 30

These types of solutions often involve special sets of whole numbers called Pythagorean triples.

A Cool Paper Folding Trick

You can fold a piece of paper into thirds using the crossed ladders idea!

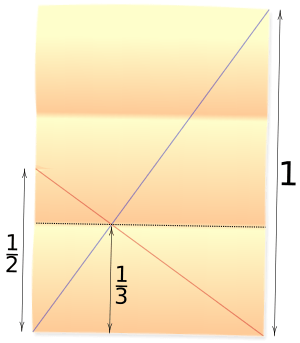
The optic equation from the crossed ladders problem can even help you fold paper! Imagine you want to fold a rectangular piece of paper into three equal parts. You can use this trick:

1. Fold the left side of the paper in half. Just make a small pinch mark at the halfway point. 2. Draw an imaginary line from this pinch mark to the opposite bottom corner (like the red line in the picture). 3. Draw another imaginary line, which is the diagonal of the whole paper (like the blue line). 4. Where these two lines cross, that point is exactly one-third of the way up from the bottom edge! 5. You can then fold the top edge of the paper down to meet this crossing point. This will give you a perfect fold into thirds.

This works because of the optic equation:

• If the full height of the paper is 1 unit, and the pinch mark is at 1/2 height, then the equation becomes: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tfrac{1}{1/2} + \tfrac{1}{1} = \tfrac{1}{h}
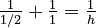
• This simplifies to: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2 + 1 = \tfrac{1}{h}
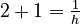
• So, 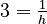Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 3 = \tfrac{1}{h} , which means Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): h = \tfrac{1}{3} .

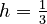You can use the same idea to fold paper into fifths, ninths, or other fractions! For example, to fold into fifths, you would fold the left side into quarters (1/4 mark) instead of halves.

Images for kids

• 

  This chart shows different solutions to the crossed ladders problem.