Nth root facts for kids

Pascal's Triangle showing P(4,1) = 4.

The nth root of a number is like solving a puzzle. You are looking for a number that, when multiplied by itself a certain number of times, gives you the original number. Imagine you have a number, let's call it r. The nth root of r is a number, let's call it k, that makes this true:

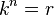
Here, 'n' tells you how many times k is multiplied by itself. For example, if n is 2, you multiply k by itself 2 times (k × k). If n is 3, you multiply k by itself 3 times (k × k × k).

We write the nth root using a special symbol: . The little 'n' above the root symbol is called the index, and r (the number inside) is called the radicand.

What is an Nth Root?

An nth root helps us find a base number when we know the result of it being multiplied by itself many times. It's the opposite of exponentiation. For example, if you know that 3 multiplied by itself 2 times (3 x 3) equals 9, then the 2nd root (or square root) of 9 is 3.

Understanding the Index 'n'

The index 'n' tells you which root you are looking for.

• If n = 2, it's a square root.
• If n = 3, it's a cube root.
• If n = 4, it's a fourth root, and so on.

When 'n' is 2 (for a square root), we usually don't write the '2' above the root symbol. So, 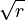means the square root of r.

Examples of Nth Roots

Let's look at some common examples to make this clearer.

Square Roots

The square root of a number is the value that, when multiplied by itself, gives the original number.

• The square root of 25 is 5, because 5 × 5 = 25. We write this as .
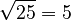• The square root of 100 is 10, because 10 × 10 = 100. We write this as .

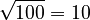Square roots are often used when working with areas of squares. If a square has an area of 36 square units, its side length is 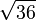, which is 6 units.

Cube Roots

The cube root of a number is the value that, when multiplied by itself three times, gives the original number.

• The cube root of 8 is 2, because 2 × 2 × 2 = 8. We write this as .
• The cube root of 64 is 4, because 4 × 4 × 4 = 64. We write this as .

Cube roots are useful when dealing with the volume of cubes. If a cube has a volume of 27 cubic units, its side length is , which is 3 units.

Why Are Nth Roots Important?

Nth roots are not just for math class; they are used in many real-world situations.

• Geometry: Finding the side lengths of squares or cubes when you know their area or volume.
• Engineering: Calculating sizes or strengths in designs.
• Finance: Understanding growth rates over time.
• Science: Solving problems in physics and chemistry.

They help us reverse calculations and find missing pieces of information in various problems.

See also

In Spanish: Radicación para niños