Cyclomatic complexity Facts for Kids

Cyclomatic complexity is a way to measure how complicated a computer program is. Imagine a map of all the different paths your program can take when it runs. Cyclomatic complexity counts how many unique, independent paths there are through that program's code. It was created by Thomas J. McCabe, Sr. in 1976.

This measurement helps us understand how hard a program might be to test or fix. It can be used for a whole program or just a small part, like a single function or a specific section of code.

One way to test software, called basis path testing, uses this idea. It suggests that you should test each of these independent paths. This means the number of tests you need might be equal to the program's cyclomatic complexity.

What is Cyclomatic Complexity?
- How Do We Measure It?
  - Paths Through the Code
  - Using Graphs to Count
- Why is it Important?
See also

What is Cyclomatic Complexity?

Cyclomatic complexity helps us understand how many different choices or decisions a program makes. Think of it like a choose-your-own-adventure book. Each time you make a choice, the story can go in a new direction. In programming, these choices are made by things like "if" statements or loops.

How Do We Measure It?

There are a few ways to figure out a program's cyclomatic complexity. One common way is to count the number of independent paths through the code.

Paths Through the Code

If a program has no choices (like an "if" statement or a loop), it has only one path. Its complexity would be 1. If a program has one simple "if" statement, it has two paths: one if the "if" condition is true, and another if it's false. Its complexity would be 2. If you have two "if" statements nested inside each other, or one "if" statement with two conditions (like "if A AND B"), the complexity goes up.

Using Graphs to Count

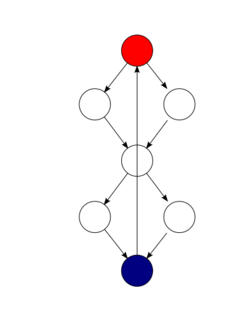
Another way to measure cyclomatic complexity is by looking at something called a control-flow graph. This is like a map of the program's steps.

A control-flow graph of a simple program. The program starts at the red circle, then goes into a loop (the three circles below the red one). After the loop, there's a choice (the group below the loop), and then the program finishes at the blue circle. This graph has 9 connections (edges), 8 steps (nodes), and 1 main part (connected component). So, its cyclomatic complexity is calculated as 9 − 8 + 2×1 = 3.

In this graph:

Nodes are like the steps or blocks of commands in your program.
Edges are the arrows that show how the program moves from one step to the next.

The complexity (let's call it M) can be found using this formula: 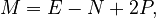$M = E - N + 2P,$ Where:

E = the number of edges (connections) in the graph.
N = the number of nodes (steps) in the graph.
P = the number of separate parts of the graph (for one program, P is usually 1).

So, for a single program, the formula often simplifies to: 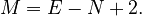$M = E - N + 2.$

This is the same program, but shown in a slightly different way where the end point connects back to the start. This graph has 10 connections (edges), 8 steps (nodes), and 1 main part. Using a different formula (10 − 8 + 1), it also gives a complexity of 3.

For programs that are well-structured (meaning they have one clear start and one clear end), the cyclomatic complexity is often equal to the number of decision points (like "if" statements or loops) plus one.

Why is it Important?

Cyclomatic complexity helps programmers and testers in several ways.

Making Code Simpler

One of the first uses of cyclomatic complexity was to help programmers keep their code from becoming too complicated. Experts suggest that if a part of a program gets too complex (for example, a complexity score over 10), it should be broken down into smaller, simpler parts. This makes the code easier to understand and manage.

Testing Your Programs

This measurement is very useful for testing software. A higher complexity number means there are more paths through the code, which means you need more tests to make sure everything works correctly.

For example, if you have a program with two "if-then-else" statements one after another:

if (c1())
    f1();
else
    f2();

if (c2())
    f3();
else
    f4();

This is the control-flow graph for the code above. The red circle is where the program starts, and the blue circle is where it ends. The end has been connected back to the start to make it a "strongly connected" graph for calculation purposes.

In this example, you might need at least 3 tests to cover all the important paths, even though there are 4 possible combinations of choices. If the complexity is higher, you need even more tests.

It's not always possible to test every single path in a complex program because the number of paths can grow very quickly. But cyclomatic complexity gives a good idea of how many tests are needed to get good coverage.

Finding Bugs

Studies have looked at whether programs with higher cyclomatic complexity tend to have more bugs. Many studies show that there is a connection: parts of programs that are more complex often have more defects. This makes sense because more complex code is harder to understand and test thoroughly.

However, it's also true that larger programs tend to be more complex and have more bugs. So, while reducing complexity is a good goal, it's not the only thing that helps reduce errors. Still, many safety standards for software suggest keeping code complexity low.

Cyclomatic complexity facts for kids

Contents