Determinant facts for kids
A determinant is a special number that comes from a square matrix. Think of it as a secret code that tells you how the matrix acts. You can figure out this number using the numbers inside the matrix. We write the determinant of a matrix A as 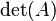 or
or  .
.
Contents
What is a Singular Matrix?
A matrix can have an inverse matrix only if its determinant is not zero. If the determinant is not zero, the matrix is called invertible. This means you can "undo" what the matrix does.
If the determinant is zero, the matrix is called non-invertible or singular. A singular matrix "flattens" things. Imagine a 3D box becoming a flat 2D shape, or a 2D square becoming a straight line. When this happens, the "volume" or "area" becomes zero. You can't easily get the original shape back.
How to Calculate a Determinant
There are different ways to find a determinant. Here are some common methods.
Formulas for Small Matrices
For very small matrices, the formulas are simple:
- For a 1x1 matrix (just one number):
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \det\begin{bmatrix}a\end{bmatrix} = a
- For a 2x2 matrix:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \det\begin{bmatrix}a&b\\c&d\end{bmatrix} = ad-bc You multiply the numbers on the main diagonal (Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a \times d ) and subtract the product of the numbers on the other diagonal (Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): b \times c ).
- For a 3x3 matrix, the formula is a bit longer:
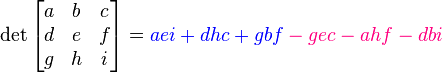 You can use the Rule of Sarrus (look at the image) to help you remember this formula. It involves multiplying numbers along specific diagonal lines.
You can use the Rule of Sarrus (look at the image) to help you remember this formula. It involves multiplying numbers along specific diagonal lines.
Cofactor Expansion Method
For bigger matrices, finding the determinant is more complex. One common way is called cofactor expansion.
Let's say you have an 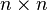 matrix (meaning it has
matrix (meaning it has  rows and
rows and  columns). 1. First, pick any row or column in the matrix. 2. For each number
columns). 1. First, pick any row or column in the matrix. 2. For each number 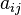 in that row or column, you need to find its cofactor
in that row or column, you need to find its cofactor  . 3. The determinant of the matrix is the sum of each number multiplied by its cofactor. So,
. 3. The determinant of the matrix is the sum of each number multiplied by its cofactor. So, 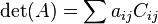 .
.
To find a cofactor  : 1. Remove (or "erase") the row
: 1. Remove (or "erase") the row 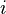 and column
and column 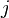 that the number
that the number 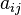 is in. 2. This leaves you with a smaller matrix, called
is in. 2. This leaves you with a smaller matrix, called 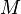 . 3. The cofactor
. 3. The cofactor  is then
is then 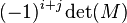 . The Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (-1)^{i+j} part means you multiply by 1 or -1 depending on if Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): i+j is even or odd.
. The Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (-1)^{i+j} part means you multiply by 1 or -1 depending on if Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): i+j is even or odd.
Here is an example using cofactor expansion on the first column of a 3x3 matrix: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{align} \det \begin{bmatrix}{\color{red}1}&3&2\\{\color{red}2}&1&1\\{\color{red}0}&3&4\end{bmatrix} \end{align} We pick the first column (numbers are 1, 2, and 0).
- For the number 1 (in row 1, column 1):
* Remove row 1 and column 1. The remaining matrix is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix}1&1\\3&4\end{bmatrix} . * Its determinant is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (1 \times 4) - (1 \times 3) = 4 - 3 = 1 . * The cofactor is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (-1)^{1+1} \times 1 = 1 \times 1 = 1 .
- For the number 2 (in row 2, column 1):
* Remove row 2 and column 1. The remaining matrix is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix}3&2\\3&4\end{bmatrix} . * Its determinant is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (3 \times 4) - (2 \times 3) = 12 - 6 = 6 . * The cofactor is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (-1)^{2+1} \times 6 = -1 \times 6 = -6 .
- For the number 0 (in row 3, column 1):
* Remove row 3 and column 1. The remaining matrix is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix}3&2\\1&1\end{bmatrix} . * Its determinant is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (3 \times 1) - (2 \times 1) = 3 - 2 = 1 . * The cofactor is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (-1)^{3+1} \times 1 = 1 \times 1 = 1 .
Now, we add them up: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{align} &= ({\color{red}1} \cdot 1) + ({\color{red}2} \cdot (-6)) + ({\color{red}0} \cdot 1) \\ &= 1 - 12 + 0 \\ &= -11. \end{align}
A helpful trick: If you choose a row or column that has many zeros, the calculation becomes much easier. This is because if 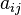 is 0, then Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a_{ij} \times C_{ij} will also be 0, so you don't need to calculate that cofactor.
is 0, then Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a_{ij} \times C_{ij} will also be 0, so you don't need to calculate that cofactor.
Related pages
See also
 In Spanish: Determinante (matemática) para niños
In Spanish: Determinante (matemática) para niños


