kids encyclopedia robot

Orbital eccentricity facts for kids

Kids Encyclopedia Facts
OrbitalEccentricityDemo
Examples of four orbital trajectories with different eccentricities

In space science, orbital eccentricity tells us how much the path of an object in space is different from a perfect circle. Think of it like how "squashed" or "stretched" an orbit is.

This number, called eccentricity (often written as e), helps describe all kinds of paths objects take around each other. These paths can be circles, ovals (called ellipses), or even open paths like parabolas or hyperbolas.

What Eccentricity Means

The value of e tells us the exact shape of an orbit:

  • For circular orbits: e is exactly zero. This means the object stays the same distance from what it's orbiting.
  • For elliptical orbits: e is more than zero but less than 1. Most planets in our solar system have elliptical orbits, meaning their distance from the Sun changes a little.
  • For parabolic paths: e is exactly 1. This is an open path, meaning the object will approach and then leave the central body, never returning.
  • For hyperbolic paths: e is more than 1. This is also an open path, but the object moves even faster and takes a wider turn as it passes by.

How to Find Eccentricity

Scientists use a special formula to calculate an object's eccentricity:

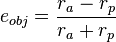
e_{obj}=\frac {r_a-r_p} {r_a+r_p}

In this formula:

  • eobj is the eccentricity of the object.
  • ra is the apoapsis. This is the farthest point in the object's orbit from the central body.
  • rp is the periapsis. This is the closest point in the object's orbit to the central body.

These two points, the farthest and closest, are together called the "apsides" of the orbit.

Images for kids

  • Animation of Orbital eccentricity

    Elliptic orbit by eccentricity       0.0 ·       0.2 ·       0.4 ·       0.6 ·       0.8

  • Eccentricity rocky planets

    Plot of the changing orbital eccentricity of Mercury, Venus, Earth, and Mars over the next 50000 years. The arrows indicate the different scales used, as the eccentricities of Mercury and Mars are much greater than those of Venus and Earth. The 0 point on this plot is the year 2007.

See also

Kids robot.svg In Spanish: Excentricidad orbital para niños

kids search engine
All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:
Orbital eccentricity Facts for Kids. Kiddle Encyclopedia.