Graph (discrete mathematics) facts for kids
A graph is a special kind of picture or model that shows how different things are connected. Think of it like a map! In a graph, the "things" are called vertices (or nodes or points), and the "connections" between them are called edges (or links or lines).
You can draw a graph by putting dots or circles for the vertices. Then, you draw lines or curves between the dots to show the edges. Graphs are a big part of a math area called discrete mathematics.
Edges can be either one-way or two-way. For example, imagine people at a party. If two people shake hands, that's a two-way connection (undirected edge), because if person A shakes B's hand, B also shakes A's hand. But if person A owes money to person B, that's a one-way connection (directed edge), because B might not owe money back to A.
The idea of a "graph" in this math sense was first used by J. J. Sylvester in 1878. He saw a link between math and how chemicals are structured.
Contents
What Are Graphs?
There are a few ways to define graphs, but here are the main types you'll learn about.
Undirected Graphs
An undirected graph is made of two main parts:
- A set of vertices (the points or dots).
- A set of edges that connect pairs of these vertices. These connections are two-way.
For an edge connecting vertex x and vertex y, we say x and y are the endpoints of that edge. The edge "joins" them. A vertex might not be connected to any other vertex at all.
Sometimes, a graph can have "multiple edges" between the same two vertices. This is like having two different roads connecting the same two towns. These are called multigraphs.
Graphs can also have loops, which are edges that connect a vertex to itself. Imagine a road that starts and ends at the same town!
Most of the time, when we talk about graphs, we mean finite graphs. This means they have a limited number of vertices and edges.
- The order of a graph is simply how many vertices it has.
- The size of a graph is how many edges it has.
- The degree of a vertex is the number of edges connected to it. If there's a loop, it counts twice!
Two vertices are called adjacent if they are connected by an edge.
Directed Graphs
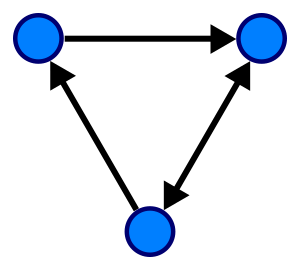
A directed graph (or digraph) is a graph where the edges have a direction. Think of them as one-way streets.
In a directed graph:
- You still have a set of vertices.
- You have a set of directed edges (also called arrows or arcs). Each edge goes from one vertex to another.
For an edge going from vertex x to vertex y, x is called the tail and y is called the head. The edge "joins" x and y. Just like with undirected graphs, a vertex might not be part of any edge.
Directed graphs can also have "multiple edges" if more than one arrow goes from the same tail to the same head. They can also have "loops" if an arrow starts and ends at the same vertex.
Directed graphs are great for modeling things like social media networks, where one person follows another (but not necessarily the other way around).
Mixed Graphs
A mixed graph is a graph that has both undirected (two-way) and directed (one-way) edges. It's like a city with both two-way streets and one-way streets!
Weighted Graphs
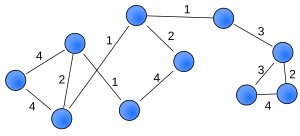
A weighted graph (or network) is a graph where each edge has a number assigned to it. This number is called a "weight."
These weights can mean different things, like:
- The cost to travel along that edge.
- The length of the connection.
- The capacity of a connection (how much can flow through it).
Weighted graphs are used in many real-world problems, such as finding the shortest path between two places (like in GPS systems) or solving the traveling salesman problem.
Different Kinds of Graphs
Oriented Graphs
An oriented graph is a special type of directed graph. It means that between any two vertices, there can be an edge in only one direction, or no edge at all. You won't find an edge from x to y AND an edge from y to x at the same time.
Regular Graphs
A regular graph is a graph where every single vertex has the exact same number of edges connected to it. For example, if every vertex has 3 edges, it's called a "3-regular graph."
Complete Graphs
A complete graph is a graph where every single pair of vertices is connected by an edge. It has all the possible connections! Imagine a group of friends where everyone is friends with everyone else.
Finite Graphs
A finite graph is a graph that has a limited number of vertices and edges. Most of the time, when people talk about graphs in math, they are talking about finite graphs. If a graph has an unlimited number of vertices or edges, it's called an infinite graph.
Connected Graphs
In an undirected graph, two vertices are connected if you can find a path (a series of edges) to get from one to the other. If you can't, they are disconnected.
A connected graph is an undirected graph where every single pair of vertices is connected. You can get from any point to any other point in the graph. If it's not connected, it's called a disconnected graph.
For directed graphs, it's a bit different:
- Strongly connected: You can go from x to y using directed edges.
- Weakly connected: You can go from x to y if you ignore the direction of the edges.
Bipartite Graphs
A bipartite graph is a graph where you can split all the vertices into two separate groups, let's call them Group W and Group X. The special rule is that edges only connect vertices from Group W to vertices in Group X. There are no edges connecting vertices within Group W, and no edges connecting vertices within Group X.
In a complete bipartite graph, every vertex in Group W is connected to every vertex in Group X.
Path Graphs
A path graph is a simple graph where the vertices are connected in a single line, one after another. Imagine a straight road with towns along it. Each town is connected only to the town before it and the town after it (except for the towns at the ends of the road).
Planar Graphs
A planar graph is a graph that you can draw on a flat surface (like a piece of paper) without any of its edges crossing over each other.
Cycle Graphs
A cycle graph is a graph where the vertices are connected in a circle. Imagine a circular road with towns along it. Each town is connected to exactly two other towns, forming a closed loop.
Trees
A tree is an undirected graph where any two vertices are connected by only one unique path. It's like a real tree with branches, where there are no closed loops (cycles). If you remove any edge from a tree, it becomes disconnected.
A forest is a collection of trees. It's an undirected graph that has no cycles at all.
Polytrees
A polytree is a directed graph that is like a tree, but with directed edges. It means there are no cycles, and if you ignore the directions of the edges, it would be a tree.
How Graphs Are Used
Graphs are super useful in many areas:
- Computer Science: They help represent how information is linked, like in conceptual graphs or how finite state machines work.
- Social Networks: They can model who follows whom on platforms like Twitter.
- Maps and Navigation: Weighted graphs are used to find the shortest routes in GPS systems.
- Biology: They can show relationships between genes or proteins.
Graph Operations
You can do different "operations" to create new graphs from existing ones:
- Unary operations change one graph into another. For example, you can remove an edge, or create a "line graph" where the old edges become new vertices.
- Binary operations combine two graphs to make a new one. This is like joining two separate networks together.
Generalizations
Graphs can be made even more complex:
- In a hypergraph, an edge can connect more than two vertices at once.
- Graphs are also used in geographic information systems (GIS) to analyze road networks or utility grids.
Images for kids
See also
 In Spanish: Grafo para niños
In Spanish: Grafo para niños
 | James Van Der Zee |
 | Alma Thomas |
 | Ellis Wilson |
 | Margaret Taylor-Burroughs |