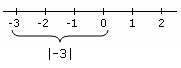Inequality Facts for Kids

Inequality in math is all about comparing numbers or expressions that aren't exactly the same. Think of it like saying one thing is bigger, smaller, or at least as big as another.

Here are the main ways we show inequality:

Smaller than: When you see `a < b`, it means that a is smaller than b.
Bigger than: When you see `a > b`, it means that a is bigger than b.
Not smaller than: If you see `a ≥ b`, it means a is either bigger than b or exactly equal to b. So, a is not smaller than b.
Not bigger than: If you see `a ≤ b`, it means a is either smaller than b or equal to b. So, a is not bigger than b.

Sometimes, "inequality" also refers to a math statement that uses these symbols to compare two expressions.

Understanding Inequalities in Math
Types of Inequalities
How to Solve Inequalities
Examples of Solving Inequalities
Related pages
Images for kids
See also

Understanding Inequalities in Math

Inequality 1 This picture shows the solution for the inequality x+4>12 on a number line.

In math, an inequality compares two values that are not equal. It tells us if one value is greater than, less than, or possibly equal to another.

When you "solve" an inequality, you're trying to find all the numbers that make the statement true. For example, if you have `x + 4 > 12`, you want to find all the possible values for 'x' that make this statement correct. If you put a number in for 'x' and the statement is true, then that number is a solution!

Solving inequalities is a bit like solving regular equations, but there are some special rules. Inequalities can often have many solutions, not just one. We usually look for solutions that are real numbers.

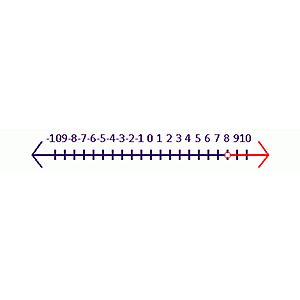
Let's look at an example: `x + 4 > 12`. To solve this, you want to get 'x' by itself. You can subtract 4 from both sides: `x + 4 - 4 > 12 - 4` `x > 8` This means any number greater than 8 is a solution. A number line (like in Inequality 1) is a great way to show all these possible solutions.

Types of Inequalities

Linear Inequality This graph shows an example of a linear inequality.

There are several different types of inequalities you might learn about:

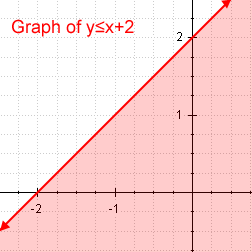
Linear Inequalities: These are like linear equations, but they use inequality symbols (`<`, `>`, `≤`, `≥`) instead of an equals sign. If you were to replace the inequality symbol with an equals sign, you'd get a straight line when you graph it.
Combined Inequalities: Sometimes you have more than one inequality that needs to be true at the same time. To find the solutions, you look for the numbers that satisfy all the inequalities.
Inequalities with Absolute Values: These involve the absolute value of a number, which is its distance from zero (always a positive value). For example, `|x| < 5` means 'x' can be any number between -5 and 5.
Polynomial Inequalities: These involve polynomials, which are expressions with variables raised to different powers (like `x² + 2x - 3`). Their graphs are smooth curves without any sudden jumps or breaks.
Rational Inequalities: These are inequalities where one polynomial is divided by another polynomial. Their graphs might have breaks where the bottom part (denominator) of the fraction becomes zero.

Absolute Value This picture shows the absolute value, which is the distance from zero on a number line.

How to Solve Inequalities

An example of adding numbers to both sides of an inequality.

Solving inequalities often involves similar steps to solving equations. Here are four common ways to work with them:

Add or Subtract: You can add or subtract the same number from both sides of an inequality without changing its direction.
Swap Sides: If you swap the sides of an inequality, you must also reverse the direction of the inequality symbol. For example, if `a < b`, then `b > a`.
Multiply: You can multiply both sides by the same positive number without changing the direction of the inequality.
Divide: You can divide both sides by the same positive number without changing the direction of the inequality.

There's a very important rule to remember:

When you multiply or divide both sides of an inequality by a negative number, you MUST reverse the direction of the inequality symbol!

This image shows how multiplying by a negative number reverses the inequality symbol.

Usually, solving an inequality takes two main steps: 1. Simplify the inequality using addition or subtraction to get terms with the variable on one side. 2. Simplify further using multiplication or division to get the variable by itself.

Examples of Solving Inequalities

Inequality 2 This number line shows the solution for the inequality -6y<-12.

An inequality is a math statement that shows two values are not equal. For example, `a ≠ b` means that a is not equal to b. The main difference between an equation and an inequality is the symbol used: inequalities use symbols like `<`, `>`, `≤`, or `≥` instead of an equals sign (`=`).

Let's look at an example where the special rule for negative numbers comes into play. Start with the true statement: `-6y < -12`. To solve for 'y', we need to divide both sides by -6. Since we are dividing by a negative number (-6), we must reverse the inequality symbol: `-6y / -6 > -12 / -6` `y > 2`

So, the correct answer is `y > 2`. This means any number greater than 2 will make the original statement true.

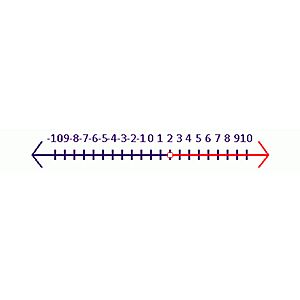
When you show solutions on a number line (like in Inequality 2):