Absolute value facts for kids
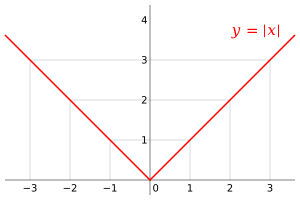
In mathematics, the absolute value (also called modulus) of a number tells you its distance from zero. It doesn't matter if the number is positive or negative; the absolute value is always a positive value or zero.
We write the absolute value of a number, like x, using two vertical bars: |x|.
For example:
- The absolute value of 3 is 3. We write this as .
- The absolute value of -3 is also 3. We write this as .
- The absolute value of 0 is 0. We write this as .
Think of it like walking on a number line. If you start at zero and walk to 5, you've walked 5 steps. If you walk to -5, you've still walked 5 steps. The absolute value is the number of steps, not the direction.
For real numbers, the absolute value is defined like this:
- If a number x is zero or positive (x ≥ 0), its absolute value is x.
- If a number x is negative (x < 0), its absolute value is -x (which makes it positive).
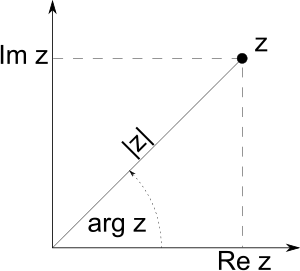
For complex numbers, the absolute value is also their distance from the origin (0,0) on a special graph called the complex plane. If you have a complex number like x + iy, its absolute value is found using the formula:
Contents
Properties of Absolute Value
The absolute value has several important rules or "properties" that help us use it in math problems.
For Real Numbers
For any real number a, the absolute value |a| has these main properties:
- Always Positive or Zero:
|a| ≥ 0 This means the absolute value of any number is always positive or zero. It can never be a negative number.
- Zero Only for Zero:
The only number whose absolute value is zero is zero itself.
- Multiplication Rule:
When you multiply two numbers, the absolute value of their product is the same as multiplying their individual absolute values. For example, . And .
- Triangle Inequality:
|a + b| ≤ |a| + |b| This property is called the "triangle inequality." It means the absolute value of the sum of two numbers is always less than or equal to the sum of their individual absolute values.
Other useful properties include:
- Absolute Value of Absolute Value:
Taking the absolute value of an absolute value doesn't change anything.
- Opposite Numbers:
The absolute value of a number is the same as the absolute value of its opposite. For example, and .
- Division Rule:
(if b is not 0) Similar to multiplication, the absolute value of a division is the same as dividing their individual absolute values.
Solving Inequalities
Absolute values are often used in inequalities. Here are two important rules:
- |a| ≤ b means that -b ≤ a ≤ b
- |a| ≥ b means that a ≤ -b or b ≤ a
Let's look at an example: Suppose you need to solve |x - 3| ≤ 9. Using the first rule above, this means: -9 ≤ x - 3 ≤ 9 Now, add 3 to all parts of the inequality: -9 + 3 ≤ x - 3 + 3 ≤ 9 + 3 -6 ≤ x ≤ 12 So, any number x between -6 and 12 (including -6 and 12) will satisfy the original inequality.
For Complex Numbers
For a complex number , where x is the real part and y is the imaginary part, the absolute value (or modulus) is: This formula comes from the Pythagorean theorem, as the complex number can be seen as a point (x,y) on a graph, and its distance from the origin (0,0) is the hypotenuse of a right triangle.
See also
 In Spanish: Valor absoluto para niños
In Spanish: Valor absoluto para niños