Hooper's paradox facts for kids
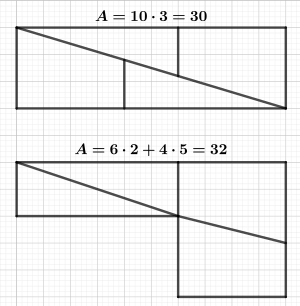
Hooper's paradox is a cool trick of the eye that makes you think something impossible is happening. It's a type of paradox where something seems wrong, but there's a simple explanation. Imagine you have a shape with a certain size (like 32 square units). You cut it into four pieces. Then, you put those same pieces back together, but they form a new shape (a rectangle) that seems to have a different size (like only 30 square units)! It looks like 2 square units just vanished into thin air!
How the Trick Works
At first glance, Hooper's paradox looks like magic. How can pieces from a 32-unit shape suddenly make a 30-unit shape? Did some area just disappear?
The secret is in the details of the shapes. If you look very closely at the triangles used in the original shape and the rectangle, you'll notice they are not exactly the same.
When the pieces are rearranged to form the rectangle, the triangles actually overlap a tiny bit. This overlap creates a small, hidden shape in the middle. This hidden shape is a parallelogram (a four-sided shape with two pairs of parallel sides).
This small, hidden parallelogram is exactly the "missing" area. Its size is 2 square units. So, the original 32 square units are still there. They are just arranged differently, with a small part overlapping, making the new shape appear smaller. It's a clever way to fool your eyes!
See also
In Spanish: Paradoja de Hooper para niños
