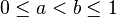Inequation facts for kids
In mathematics, an inequation is a statement that shows how two values or expressions are related using an inequality sign. It's like saying one thing is bigger than, smaller than, or not equal to another.
Think of it like a balance scale. An equation means both sides are perfectly balanced (equal). An inequation means one side is heavier or lighter than the other, or simply not the same.
Here are some common inequality signs you'll see in inequations:
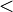 (less than)
(less than)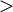 (greater than)
(greater than) (less than or equal to)
(less than or equal to)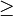 (greater than or equal to)
(greater than or equal to)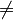 (not equal to)
(not equal to)
For example:
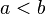 means 'a' is less than 'b'.
means 'a' is less than 'b'. means the sum of x, y, and z is less than or equal to 1.
means the sum of x, y, and z is less than or equal to 1. means 'n' is greater than 1.
means 'n' is greater than 1.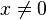 means 'x' is not equal to 0.
means 'x' is not equal to 0.
Sometimes, the words "inequation" and "inequality" are used to mean the same thing. Other times, "inequation" is used specifically for statements where things are "not equal to" (like 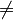 ).
).
Contents
Chains of Inequalities: Linking Statements
Sometimes, you'll see several inequations linked together in a "chain." This is a short way to write multiple inequality statements at once.
For example, the chain:
This actually means three things at the same time:
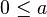 (0 is less than or equal to 'a')
(0 is less than or equal to 'a')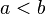 ('a' is less than 'b')
('a' is less than 'b')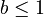 ('b' is less than or equal to 1)
('b' is less than or equal to 1)
When you link them this way, it also tells you other things. For instance, in the example above, it means that 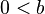 (0 is less than 'b') and
(0 is less than 'b') and 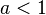 ('a' is less than 1).
('a' is less than 1).
However, not all chains imply relationships between the very first and very last parts. For example, 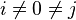 means
means 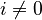 AND
AND 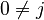 . It does not mean that
. It does not mean that 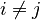 .
.
Solving Inequations: Finding the Right Values
Just like you solve an equation to find the value of an unknown, you can also solve inequations. When you solve an inequation, you are looking for all the values (numbers, functions, or sets) that make the inequation true.
These inequations often have one or more "unknowns." These are like empty spaces or variables (often shown as letters like 'x' or 'y') that you need to fill in. A solution is any value you can put in place of the unknown that makes the inequation correct.
For example, if you have the inequation 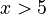 , any number greater than 5 (like 6, 7, 10.5, or 100) would be a solution. There isn't just one answer, but a whole range of answers!
, any number greater than 5 (like 6, 7, 10.5, or 100) would be a solution. There isn't just one answer, but a whole range of answers!
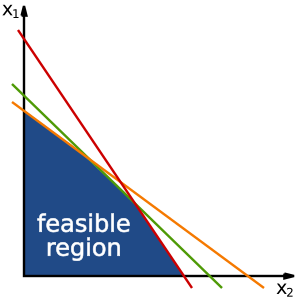
Sometimes, you might have a group of inequations that all need to be true at the same time. The picture on the right shows an example of this. The blue shaded area represents all the points (values for 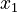 and
and 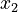 ) that satisfy all the inequations in that group. This area is called a "feasible region."
) that satisfy all the inequations in that group. This area is called a "feasible region."
Computers can be very helpful in solving complex inequations, especially when there are many of them. Programs and algorithms, like the simplex algorithm, are used to find the best possible solutions, especially in fields like Linear programming.
Combining Inequations: More Complex Problems
Sometimes, one inequation can be equal to a combination of several simpler inequations. This often happens when you're dealing with special functions, like square roots.
For example, the inequation 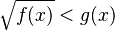 might look simple, but to solve it correctly, you need to make sure three things are true at the same time:
might look simple, but to solve it correctly, you need to make sure three things are true at the same time:
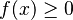 (The number inside the square root must be zero or positive.)
(The number inside the square root must be zero or positive.)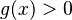 (The number on the other side must be positive.)
(The number on the other side must be positive.) (The original relationship holds when you square both sides.)
(The original relationship holds when you square both sides.)
This shows how one inequation can hide several conditions that all need to be met for it to be true.
See also
 In Spanish: Inecuación para niños
In Spanish: Inecuación para niños
- Equation
- Equals sign
- Inequality (mathematics)
- Relational operator