Katrin Leschke facts for kids
Katrin Leschke (born in 1968) is a mathematician from Germany. She is an expert in a field called differential geometry. This area of math studies shapes and spaces using calculus.
Katrin Leschke is also known for her work on quaternionic analysis. This is a special type of math that uses numbers called quaternions. She also studies Willmore surfaces, which are specific kinds of curved shapes.
She works in England at the University of Leicester. There, she is a reader in mathematics. This is a senior teaching and research position. She also leads a group called the "Maths Meets Arts Tiger Team." This team helps make math more popular and fun for everyone. She also led an international project called "m:iv" which focused on minimal surfaces. These are shapes that have the smallest possible surface area for their boundaries.
About Her Life and Work
Katrin Leschke studied at the Technische Universität Berlin in Germany. She earned her first degree there. Later, she completed her PhD in 1997 at the same university. Her PhD project was about complex math topics like "Isoparametric Manifolds." Her supervisors were Dirk Ferus and Ulrich Pinkall.
After her PhD, she continued her research at Technische Universität Berlin until 2002. She then worked as a visiting assistant professor at the University of Massachusetts Amherst in the United States from 2002 to 2005.
From 2005 to 2007, she was a researcher and temporary associate professor at the University of Augsburg in Germany. While there, she completed her "habilitation." This is a special qualification in some European countries that allows someone to teach at a university at a high level. She worked with Katrin Wendland during this time.
In 2007, Katrin Leschke joined the University of Leicester as a new lecturer. She became a reader there in 2016.
Her Book
Katrin Leschke is one of the authors of a book titled Conformal Geometry of Surfaces in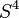 
and Quaternions. This book was published by Springer in 2002. It helps explain the ideas behind quaternionic analysis.
