Killer sudoku facts for kids
Killer Sudoku (also called Sumdoku or Addoku) is a fun puzzle game. It mixes parts of regular sudoku and another puzzle called kakuro. Don't let the name "Killer" scare you! Some Killer Sudoku puzzles are actually easier than normal Sudoku. This is especially true if you are good at quick math. But the hardest ones can take many hours to solve!
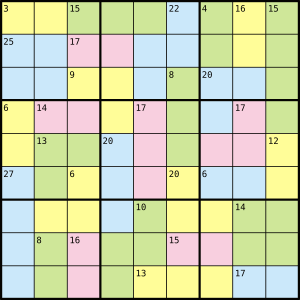
You can see an example puzzle on the right. It uses colors to show special groups of cells. But usually, these puzzles are printed in black and white. These groups are marked with thin dotted lines. They are called "cages."
Contents
How to Play Killer Sudoku
The goal of Killer Sudoku is to fill a grid with numbers from 1 to 9. You need to follow these rules:
- Every row must have each number from 1 to 9 exactly once.
- Every column must have each number from 1 to 9 exactly once.
- Every 3x3 box (also called a "nonet") must have each number from 1 to 9 exactly once.
- Each "cage" (a group of cells outlined by dotted lines) has a small number in its corner. The numbers inside that cage must add up to this small number.
- No number can appear more than once inside a single cage. This means a cage can't have more than 9 cells.
Some special Killer Sudoku puzzles, called 'Killer X', have an extra rule. In these, each of the two long diagonal lines must also contain each number from 1 to 9 exactly once.
What are Cages?
In Killer Sudoku, a "cage" is a group of cells. These cells are connected and are usually outlined by a dotted line. Each cage has a target sum. This sum is the small number written in one of its corners. The numbers you place inside that cage must add up to this target sum. Also, you cannot repeat any number within a single cage.
Solving Strategies for Killer Sudoku
Solving Killer Sudoku can be tricky, but there are some smart ways to figure them out.
Start with Extreme Sums
It's often best to start with cages that have very high or very low sums. Why? Because these cages have fewer possible number combinations.
For example:
- A cage with 5 cells that adds up to 34 can only be the numbers 4, 6, 7, 8, and 9. There's only one way!
- But a cage with 5 cells that adds up to 25 has twelve possible combinations.
When you first start a puzzle, look for these cages with extreme sums. Especially if they form a straight line. Knowing what numbers must be in these cells helps you figure out other cells in the same row or column. This is like "cross-hatching" to narrow down possibilities.
The Rule of 45
This is a very helpful trick! You know that all the numbers in any complete row, column, or 3x3 box (nonet) must add up to 45. This is because they all contain the numbers 1 through 9 (1+2+3+4+5+6+7+8+9 = 45).
You can use this rule to find missing numbers. Add up the sums of all the cages that are completely inside one row, column, or nonet. If there's a cell or a small group of cells not part of a cage in that area, you can figure out its sum by subtracting the cage sums from 45.
Example of the 45 Rule
Imagine a 3x3 box (nonet) on the left side of the puzzle. Let's say it has three cages inside it. These cages add up to a total of 33. Since a full nonet must add up to 45, the remaining two cells in that nonet must add up to 12 (45 - 33 = 12).
Now, let's say one of these two cells is also part of a different cage that has a sum of 6 with two other cells. This means that cell can only be 1, 2, or 3 (because if it were 4 or more, the other two cells in its cage couldn't add up to 6 without repeating numbers or going over 9).
- If it were 1, the other cell in the nonet would need to be 11 (impossible).
- If it were 2, the other cell would need to be 10 (impossible).
- So, it must be 3! And if that cell is 3, then the other cell in the nonet must be 9 (3 + 9 = 12).
Consistent Numbers in Combinations
Sometimes, a cage can have several possible combinations of numbers. Even so, one or more numbers might appear in every possible combination for that cage.
For example: A 4-cell cage that totals 13. The possible combinations are:
- (1, 2, 3, 7)
- (1, 2, 4, 6)
- (1, 3, 4, 5)
Notice that the number 1 is in all three combinations. This means that one of the cells in that cage must be a 1. This is helpful if you've already figured out that another cell in the same row, column, or 3x3 box is also a 1. Then you know the 1 in this cage has to be in a cell that is not in that same row, column, or box.
Using Complements
For larger cages (like 6, 7, or 8 cells), thinking about their "complements" can make things easier. A complement is the opposite.
- For a 6-cell cage, its complement is a 3-cell group. The sum of the 6-cell cage plus the sum of its 3-cell complement will always be 45 (the total of a 9-cell nonet).
- For a 7-cell cage, its complement is a 2-cell group.
- An 8-cell cage is missing only one digit. Its sum subtracted from 45 tells you that missing digit.
For example: A 7-cell cage adds up to 41. Its complement is a 2-cell group that adds up to 4 (because 45 - 41 = 4). A 2-cell group that sums to 4 can only be 1 and 3. This means the 7-cell cage that sums to 41 cannot contain 1 or 3. This helps you eliminate possibilities.
Cage Total Tables
These tables list the possible number combinations for different cage sums. Remember, numbers in a cage cannot repeat.
- 1 cell
- 1: 1
- 2: 2
- 3: 3
- 4: 4
- 5: 5
- 6: 6
- 7: 7
- 8: 8
- 9: 9
- 2 cells
- 3: 12
- 4: 13
- 5: 14, 23
- 6: 15, 24
- 7: 16, 25, 34
- 8: 17, 26, 35
- 9: 18, 27, 36, 45
- 10: 19, 28, 37, 46
- 11: 29, 38, 47, 56
- 12: 39, 48, 57
- 13: 49, 58, 67
- 14: 59, 68
- 15: 69, 78
- 16: 79
- 17: 89
- 3 cells
- 6: 123
- 7: 124
- 8: 125, 134
- 9: 126, 135, 234
- 10: 127, 136, 145, 235
- 11: 128, 137, 146, 236, 245
- 12: 129, 138, 147, 156, 237, 246, 345
- 13: 139, 148, 157, 238, 247, 256, 346
- 14: 149, 158, 167, 239, 248, 257, 347, 356
- 15: 159, 168, 249, 258, 267, 348, 357, 456
- 16: 169, 178, 259, 268, 349, 358, 367, 457
- 17: 179, 269, 278, 359, 368, 458, 467
- 18: 189, 279, 369, 378, 459, 468, 567
- 19: 289, 379, 469, 478, 568
- 20: 389, 479, 569, 578
- 21: 489, 579, 678
- 22: 589, 679
- 23: 689
- 24: 789
- 4 cells
- 10: 1234
- 11: 1235
- 12: 1236, 1245
- 13: 1237, 1246, 1345
- 14: 1238, 1247, 1256, 1346, 2345
- 15: 1239, 1248, 1257, 1347, 1356, 2346
- 16: 1249, 1258, 1267, 1348, 1357, 1456, 2347, 2356
- 17: 1259, 1268, 1349, 1358, 1367, 1457, 2348, 2357, 2456
- 18: 1269, 1278, 1359, 1368, 1458, 1467, 2349, 2358, 2367, 2457, 3456
- 19: 1279, 1369, 1378, 1459, 1468, 1567, 2359, 2368, 2458, 2467, 3457
- 20: 1289, 1379, 1469, 1478, 1568, 2369, 2378, 2459, 2468, 2567, 3458, 3467
- 21: 1389, 1479, 1569, 1578, 2379, 2469, 2478, 2568, 3459, 3468, 3567
- 22: 1489, 1579, 1678, 2389, 2479, 2569, 2578, 3469, 3478, 3568, 4567
- 23: 1589, 1679, 2489, 2579, 2678, 3479, 3569, 3578, 4568
- 24: 1689, 2589, 2679, 3489, 3579, 3678, 4569, 4578
- 25: 1789, 2689, 3589, 3679, 4579, 4678
- 26: 2789, 3689, 4589, 4679, 5678
- 27: 3789, 4689, 5679
- 28: 4789, 5689
- 29: 5789
- 30: 6789
- 5 cells
- 15: 12345
- 16: 12346
- 17: 12347, 12356
- 18: 12348, 12357, 12456
- 19: 12349, 12358, 12367, 12457, 13456
- 20: 12359, 12368, 12458, 12467, 13457, 23456
- 21: 12369, 12378, 12459, 12468, 12567, 13458, 13467, 23457
- 22: 12379, 12469, 12478, 12568, 13459, 13468, 13567, 23458, 23467
- 23: 12389, 12479, 12569, 12578, 13469, 13478, 13568, 14567, 23459, 23468, 23567
- 24: 12489, 12579, 12678, 13479, 13569, 13578, 14568, 23469, 23478, 23568, 24567
- 25: 12589, 12679, 13489, 13579, 13678, 14569, 14578, 23479, 23569, 23578, 24568, 34567
- 26: 12689, 13589, 13679, 14579, 14678, 23489, 23579, 23678, 24569, 24578, 34568
- 27: 12789, 13689, 14589, 14679, 15678, 23589, 23679, 24579, 24678, 34569, 34578
- 28: 13789, 14689, 15679, 23689, 24589, 24679, 25678, 34579, 34678
- 29: 14789, 15689, 23789, 24689, 25679, 34589, 34679, 35678
- 30: 15789, 24789, 25689, 34689, 35679, 45678
- 31: 16789, 25789, 34789, 35689, 45679
- 32: 26789, 35789, 45689
- 33: 36789, 45789
- 34: 46789
- 35: 56789
- 6 cells
- 21: 123456
- 22: 123457
- 23: 123458, 123467
- 24: 123459, 123468, 123567
- 25: 123469, 123478, 123568, 124567
- 26: 123479, 123569, 123578, 124568, 134567
- 27: 123489, 123579, 123678, 124569, 124578, 134568, 234567
- 28: 123589, 123679, 124579, 124678, 134569, 134578, 234568
- 29: 123689, 124589, 124679, 125678, 134579, 134678, 234569, 234578
- 30: 123789, 124689, 125679, 134589, 134679, 135678, 234579, 234678
- 31: 124789, 125689, 134689, 135679, 145678, 234589, 234679, 235678
- 32: 125789, 134789, 135689, 145679, 234689, 235679, 245678
- 33: 126789, 135789, 145689, 234789, 235689, 245679, 345678
- 34: 136789, 145789, 235789, 245689, 345679
- 35: 146789, 236789, 245789, 345689
- 36: 156789, 246789, 345789
- 37: 256789, 346789
- 38: 356789
- 39: 456789
- 7 cells
- 28: 1234567
- 29: 1234568
- 30: 1234569, 1234578
- 31: 1234579, 1234678
- 32: 1234589, 1234679, 1235678
- 33: 1234689, 1235679, 1245678
- 34: 1234789, 1235689, 1245679, 1345678
- 35: 1235789, 1245689, 1345679, 2345678
- 36: 1236789, 1245789, 1345689, 2345679
- 37: 1246789, 1345789, 2345689
- 38: 1256789, 1346789, 2345789
- 39: 1356789, 2346789
- 40: 1456789, 2356789
- 41: 2456789
- 42: 3456789
- 8 cells
- 36: 12345678
- 37: 12345679
- 38: 12345689
- 39: 12345789
- 40: 12346789
- 41: 12356789
- 42: 12456789
- 43: 13456789
- 44: 23456789
- 9 cells
- 45: 123456789
See also
 In Spanish: Addoku para niños
In Spanish: Addoku para niños