Maximum and minimum facts for kids

The maximum and minimum are important ideas in mathematics. They help us find the biggest or smallest things in a group of numbers or the highest or lowest points a function can reach. When we talk about both the maximum and minimum together, we call them extrema.

Imagine you have a set of numbers, like {2, 7, 1, 9, 5}. The maximum number in this set is 9, because it's the largest. The minimum number is 1, because it's the smallest.

We use these words in everyday life too!

• Minimum means the smallest amount you can have or do. For example, if the minimum amount of dollars you must pay for something is seven, it means you have to pay at least seven dollars. You can pay more, but not less.
• Maximum means the largest amount you can have or do. For example, if the maximum number of oranges you can juggle is five, it means you can juggle five oranges or fewer, but you cannot juggle more than five.

This graph shows a wavy line. The highest points are called local maxima, and the lowest points are called local minima.

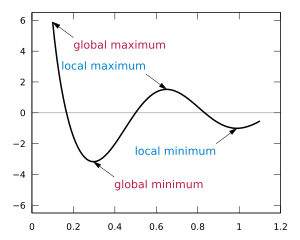
What are Local and Global Extrema?

When we look at a function (like a line on a graph), it can have different kinds of maximums and minimums:

Local Extrema

A local maximum is like the top of a small hill on a graph. It's the highest point in its immediate area, but the graph might go even higher somewhere else. A local minimum is like the bottom of a small valley. It's the lowest point in its immediate area, but the graph might go even lower somewhere else.

Global Extrema

The global maximum is the very highest point the function ever reaches across its entire graph. It's the absolute peak. The global minimum is the very lowest point the function ever reaches across its entire graph. It's the absolute lowest point.

Sometimes, a local maximum or minimum can also be a global maximum or minimum if it happens to be the highest or lowest point overall.

Finding Extrema

Finding extrema is a big part of mathematical optimization. This is a field where people try to find the best possible solution to a problem, like finding the most efficient way to do something or the least amount of material needed for a project.

For example, engineers might use these ideas to find the strongest design for a bridge (maximizing strength) or the least amount of fuel a car needs to travel a certain distance (minimizing fuel use).

Images for kids

• 

  This is a complex mathematical shape.

• MaximumParaboloid.png

  This shape shows a clear global maximum at the very top.

• 

  Here, the red dot shows a local minimum. It's the lowest point in its area, but the graph goes even lower somewhere else, so it's not the global minimum.

See also

In Spanish: Extremos de una función para niños