Napier's bones facts for kids
| Top - 0-9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Napier's bones is a cool old tool for doing math! It was invented by a Scottish mathematician named John Napier in 1617. This device helps you multiply and divide numbers, and it can even find square roots.
The way it works is based on a method called lattice multiplication. Napier also called his invention rabdology. He published his ideas about it in a book in Edinburgh.
Napier's bones make big multiplication problems easier by turning them into simple addition. They also turn division into subtraction. This tool is different from logarithms, which Napier also worked on. Instead, it uses multiplication tables broken down into parts.
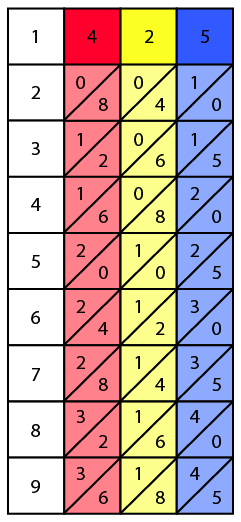
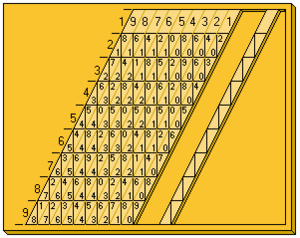
The device usually has a flat board with a raised edge. You place special rods, or "bones," inside this edge. The left side of the board has numbers from 1 to 9.
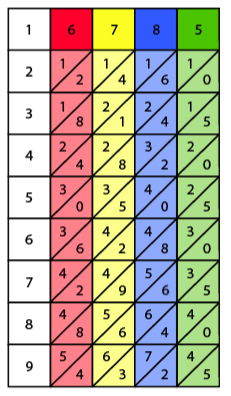
Originally, the rods were made from materials like metal, wood, or ivory. Each rod had four sides, and each side had a multiplication table carved into it. Later versions were flat, made of plastic or cardboard, and had one or two tables on them. A full set of these bones often came in a carrying case.
Each side of a rod has nine squares. All squares, except the top one, are split in half by a diagonal line. These squares show a simple multiplication table. The top square has a single digit, which Napier called the 'single'. The squares below it show multiples of that number (like 2 times, 3 times, up to 9 times). If a number is a single digit (like 4), it goes in the bottom right triangle. If it's a double-digit number (like 12), one digit goes on each side of the diagonal line.
To multiply numbers with many digits, you would need many rods. For example, to multiply 4-digit numbers, you'd need 40 rods if they were single-sided. But if you use square rods, you can fit 40 multiplication tables onto just 10 rods. Napier figured out a clever way to arrange the tables so that a set of 10 rods could represent any 4-digit number. A set of 20 rods could handle numbers up to eight digits, and 30 rods could work with 12-digit numbers!
How to Multiply with Napier's Bones
Multiplying with Napier's bones is pretty straightforward. You arrange the rods to match the number you want to multiply. Then, you read the answer from the rows, doing a little bit of addition along the way.
If you're multiplying a number by another number with many digits, you set up the rods for the larger number. You then find a separate result for each digit of the smaller number. You write these down and add them up later to get the final answer.
Let's look at some examples to see how it works!
Example 1: Multiplying by a Small Single Digit
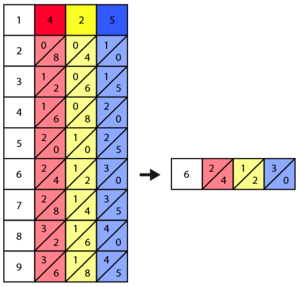
Let's calculate 425 × 6.
First, you pick out the Napier's bones for the numbers 4, 2, and 5. You place them side-by-side on the board. These bones show the larger number you want to multiply.
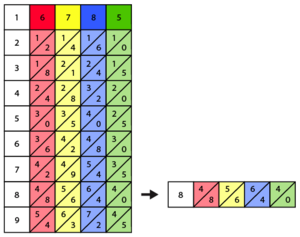
The numbers on each bone are like regular multiplication tables. For example, if you look at the 7th row of the '4' bone, you'll see 2 and 8 (meaning 28), because 7 × 4 = 28. In our example, the bones are shown as red (4), yellow (2), and blue (5).
Next, you find the row that matches the single digit you're multiplying by. In this example, we are multiplying by 6. So, you look at the 6th row across all the bones.
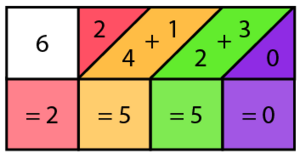
Now, you add the numbers that are next to each other along the diagonal lines. You start from the right side. The very last number on the right doesn't need to be added to anything.
Look at the diagram. You add the numbers that are between the diagonal lines. For example, the green numbers from the yellow and blue bones are added together. You write down each sum from left to right.
Following this, you get the numbers 2, 5, 5, and 0. When you put them together, the answer is 2550. So, 425 × 6 = 2550!
Example 2: Multiplying by a Larger Single Digit
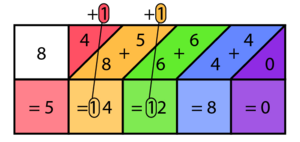
What if the numbers you add along the diagonals are 10 or more? Let's try 6785 × 8.
Just like before, you set up the bones for 6, 7, 8, and 5 on the board.
We are multiplying by 8, so we look at the 8th row.
Now, add the numbers along the diagonal columns, starting from the right. If a sum is 10 or more, you "carry over" the tens digit to the next column on the left, just like in regular addition.
After adding all the diagonal columns and carrying over, you read the numbers from left to right. This gives you 54280.
So, 6785 × 8 = 54280.
Example 3: Multiplying by a Multi-Digit Number
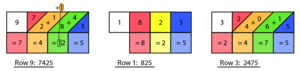
Now for a bigger challenge: 825 × 913.
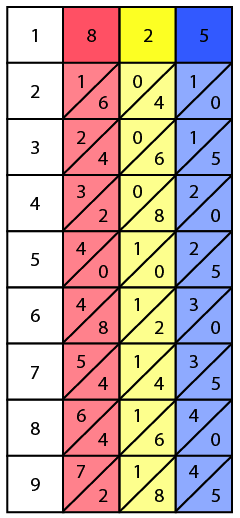
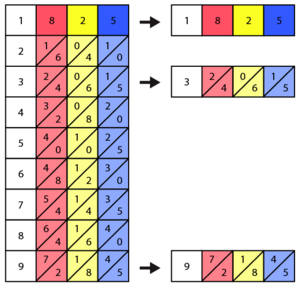
First, set up the bones for 8, 2, and 5 on the board.
Since we're multiplying by a multi-digit number (913), we'll need to look at multiple rows: the 9th row, the 1st row, and the 3rd row.
You calculate the result for each row separately, just like in the previous examples. Add the numbers along the diagonals for each row.
This gives you three intermediate results:
- For the 3rd row: 2475
- For the 1st row: 0825 (or 825)
- For the 9th row: 7425
Now, you arrange these results for a final addition, just like in long multiplication. Remember to add zeros as placeholders for each digit's place value.
- 2475 (for the 3 in 913)
- 8250 (for the 1 in 913, shifted one place left)
- 742500 (for the 9 in 913, shifted two places left)
Finally, add these numbers together: 2475 8250 +742500
753225
So, 825 × 913 = 753225.
How to Divide with Napier's Bones
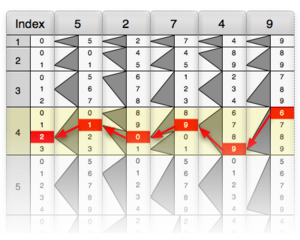
You can also use Napier's bones for division! Let's try to divide 46785399 by 96431.
First, you place the bones for the divisor (96431) on the board. Then, you find all the products of this divisor from 1 to 9 by reading the numbers on the bones.
The number we are dividing (46785399) has eight digits. The products we get from the bones (except the first one) have six digits. So, we temporarily ignore the last two digits of 46785399 (the '99'), leaving us with 467853.
Now, find the largest product from your bones that is less than 467853. In this case, it's 385724, which comes from the '4' row.
You write down '4' as the first digit of your answer (the quotient). Then, you write 385724 directly under 467853 and subtract it. 467853 - 385724 = 82129.
Now, bring down the next digit from the original number (the '9' from 46785399), making it 821299. Repeat the process: Find the largest product from your bones that is less than 821299. This is 771448, which comes from the '8' row. Write down '8' as the next digit of your quotient. Subtract 771448 from 821299. 821299 - 771448 = 49851.
Bring down the last digit (the final '9' from 46785399), making it 498519. Find the largest product less than 498519. This is 482155, from the '5' row. Write down '5' as the next digit of your quotient. Subtract 482155 from 498519. 498519 - 482155 = 16364.
Since 16364 is smaller than our divisor (96431), we stop here for integer division.
So, 46785399 divided by 96431 is 485 with a remainder of 16364. You can write this as 485 and 16364/96431.
If you need a more exact answer with decimals, you can keep going. Just add a decimal point to your quotient and add a zero to your remainder (163640). Then, continue the steps.
Extracting Square Roots
Napier's bones can even help you find square roots! For this, you use a special "square root bone" that's different from the others. It has three columns:
- The first column shows the first nine square numbers (like 1, 4, 9, 16...).
- The second column has the first nine even numbers (like 2, 4, 6, 8...).
- The last column simply has the numbers 1 to 9.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | √ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0⁄1 | 0⁄2 | 0⁄3 | 0⁄4 | 0⁄5 | 0⁄6 | 0⁄7 | 0⁄8 | 0⁄9 | 0⁄1 2 1 |
| 2 | 0⁄2 | 0⁄4 | 0⁄6 | 0⁄8 | 1⁄0 | 1⁄2 | 1⁄4 | 1⁄6 | 1⁄8 | 0⁄4 4 2 |
| 3 | 0⁄3 | 0⁄6 | 0⁄9 | 1⁄2 | 1⁄5 | 1⁄8 | 2⁄1 | 2⁄4 | 2⁄7 | 0⁄9 6 3 |
| 4 | 0⁄4 | 0⁄8 | 1⁄2 | 1⁄6 | 2⁄0 | 2⁄4 | 2⁄8 | 3⁄2 | 3⁄6 | 1⁄6 8 4 |
| 5 | 0⁄5 | 1⁄0 | 1⁄5 | 2⁄0 | 2⁄5 | 3⁄0 | 3⁄5 | 4⁄0 | 4⁄5 | 2⁄5 10 5 |
| 6 | 0⁄6 | 1⁄2 | 1⁄8 | 2⁄4 | 3⁄0 | 3⁄6 | 4⁄2 | 4⁄8 | 5⁄4 | 3⁄6 12 6 |
| 7 | 0⁄7 | 1⁄4 | 2⁄1 | 2⁄8 | 3⁄5 | 4⁄2 | 4⁄9 | 5⁄6 | 6⁄3 | 4⁄9 14 7 |
| 8 | 0⁄8 | 1⁄6 | 2⁄4 | 3⁄2 | 4⁄0 | 4⁄8 | 5⁄6 | 6⁄4 | 7⁄2 | 6⁄4 16 8 |
| 9 | 0⁄9 | 1⁄8 | 2⁄7 | 3⁄6 | 4⁄5 | 5⁄4 | 6⁄3 | 7⁄2 | 8⁄1 | 8⁄1 18 9 |
Let's find the square root of 46785399.
First, group the digits of the number into pairs, starting from the right.
- 46785399
(If you had a number like 85399, you'd group it as 085399.)
Take the leftmost group, which is 46. Look at the square root bone. Find the largest square number that is less than or equal to 46. That's 36, which is in the sixth row. So, the first digit of our answer is 6.
Now, take the number from the second column of the sixth row on the square root bone, which is 12. You'll use this on your main board.
Subtract 36 (from the first column of the sixth row) from 46. This leaves 10. Bring down the next pair of digits (78) next to the 10, making it 1078.
Your setup should look like this:
|
√46 78 53 99 = 6 − 36 10 78 |
Now, you need to find the largest number on the board (using the 12 you got earlier) that is less than 1078. You'll read the numbers from the bones, ignoring the second and third columns of the square root bone. For example, the sixth row would be read as 756 (from 06, 12, 36).
The largest number less than 1078 is 1024, which comes from the eighth row.
|
√46 78 53 99 = 68 − 36 10 78 − 10 24 54 |
So, 8 is the next digit of the square root. Subtract 1024 from 1078, which leaves 54. Bring down the next pair of digits (53), making it 5453.
Now, adjust the numbers on your board. Take the second column of the eighth row from the square root bone, which is 16. Add the first digit of 16 (which is 1) to the current number on your board (12). This makes 13. Then, add the second digit of 16 (which is 6) to the end of 13, making it 136.
Your setup now looks like this:
|
√46 78 53 99 = 68 − 36 10 78 − 10 24 54 53 |
Find the largest value on the board that is less than 5453. This is 4089, from the third row.
|
√46 78 53 99 = 683 − 36 10 78 − 10 24 54 53 − 40 89 13 64 |
The next digit of the square root is 3. Subtract 4089 from 5453, leaving 1364. Bring down the last pair of digits (99), making it 136499.
Adjust the board again. The second column of the third row on the square root bone is 6. Add this 6 to the end of the current number on the board (136), making it 1366.
Your setup now looks like this:
|
√46 78 53 99 = 683 − 36 10 78 − 10 24 54 53 − 40 89 13 64 99 |
Find the largest value on the board smaller than 136499. This is 123021, from the ninth row.
|
√46 78 53 99 = 6839 − 36 10 78 − 10 24 54 53 − 40 89 13 64 99 − 12 30 21 1 34 78 |
The next digit is 9. Subtract 123021 from 136499, leaving 13478.
Since all original digits are used, 6839 is the integer part of the square root. If you need more precision, you can add two zeros to the remainder (1347800) and continue the process.
Adjust the board again. The second column of the ninth row on the square root bone is 18. Add the first digit of 18 (1) to the current number on the board (1366), making it 1367. Then, add the second digit of 18 (8) to the end of 1367, making it 13678.
Your setup now looks like this:
|
√46 78 53 99.00 = 6839. − 36 10 78 − 10 24 54 53 − 40 89 13 64 99 − 12 30 21 1 34 78 00 |
Find the largest value on the board smaller than 1347800. This is 1231101, from the ninth row.
|
√46 78 53 99.00 = 6839.9 − 36 10 78 − 10 24 54 53 − 40 89 13 64 99 − 12 30 21 1 34 78 00 − 1 23 11 01 11 66 99 |
The first decimal digit of the square root is 9. Subtract 1231101 from 1347800, leaving 116699. You can keep adding two zeros to the remainder and repeating these steps to find more decimal places. If the remainder becomes zero, you've found the exact square root!
Rounding Up
After finding the digits you need, you can decide if the last digit should be rounded up. You don't need to find another full digit. Just append 25 to your current root (e.g., 6839925). Compare this to your last remainder (11669900). If the root with 25 appended is less than or equal to the remainder, then the next digit would be 5 or more, meaning you should round up. In our example, 6839925 is less than 11669900, so you would round up the last digit, making the root approximately 6840.0.
If you need to find the square root of a number that isn't a whole number (like 54782.917), you group the digits into pairs from the decimal point outwards. So, 54782.917 would be grouped as:
- 054782.9170
Then, you follow the same steps as before.
Diagonal Modification
In the 1800s, Napier's bones were changed to make them easier to read. The rods were made with a slant (about 65 degrees) so that the numbers you needed to add were already lined up. This meant the 'units' digit was on the right and the 'tens' digit (or zero) was on the left in each square.
This new design made it very clear which numbers to add. For example, you could immediately see that:
- 987654321 × 5 = 4938271605
Genaille–Lucas Rulers
In 1891, a person named Henri Genaille created a different version of Napier's bones. These were called Genaille–Lucas rulers. They were even cleverer because they showed you how to "carry over" numbers visually. This meant you could read the answer to simple multiplication problems directly, without having to do any extra mental math!
Here's an example: calculating 52749 × 4 = 210996.
See also
 In Spanish: Ábaco neperiano para niños
In Spanish: Ábaco neperiano para niños
- Genaille–Lucas rulers
- Pascal's calculator
- Slide rule