Slide rule facts for kids

Kids Encyclopedia Facts

The slide rule, also called a slipstick, is a special tool that helps you do math. It's like a mechanical analog computer, meaning it uses physical parts to solve problems. People mainly used slide rules for multiplication and division. They could also do more complex math like finding roots, logarithms (which help with big numbers), and trigonometry (math about triangles). However, slide rules were not used for simple addition or subtraction.

There are many kinds of slide rules. Some are long and straight (linear), while others are round (circular). They all have special markings called scales, which are used for calculations. Some slide rules were even made for specific jobs, like for aviation (flying planes) or finance (money matters). These had extra scales for those tasks.

William Oughtred and others created the slide rule in the 1600s. It was based on the idea of logarithms developed by John Napier. Before electronic calculators came along, slide rules were the most common tool for people in science and engineering. They were widely used until about 1974, when small pocket calculators became popular. These new calculators made the slide rule largely outdated.

A slide rule set up to multiply by 2. Notice how each number on the D (bottom) scale is double the number above it on the C (middle) scale.

How Slide Rules Work

At its simplest, a slide rule uses two special scales that help you multiply and divide numbers quickly. These math operations can take a lot of time and lead to mistakes if done on paper. More advanced slide rules let you do other calculations, like finding square roots, exponentials, logarithms, and trigonometric functions.

A cursor on a slide rule.

You do math by lining up a mark on the middle sliding part with a mark on one of the fixed outer parts. Then, you look at where other marks line up. The numbers next to these marks give you an approximate answer for your product, quotient, or other result.

You have to figure out where the decimal point goes in your answer yourself. This is usually done by guessing or using Scientific notation for more formal calculations. Simple Addition and subtraction are usually done in your head or on paper, not on the slide rule.

Most slide rules have three straight strips of the same length. They fit together so the middle strip can slide back and forth. The two outer strips stay fixed in place.

Some slide rules, called "duplex" models, have scales on both sides. Others, called "simplex" rules, only have scales on one side. A sliding cursor (a clear piece with a line) helps you find matching points on scales that are not next to each other. It can also help you remember an answer in the middle of a longer calculation.

Using a Slide Rule for Math

Multiplying Numbers

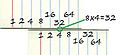
Logarithms change multiplication into addition. So, a slide rule works by adding lengths on its scales. To multiply numbers like X and Y, you move the top scale so its beginning (marked '1') lines up with X on the bottom scale. Then, you find Y on the top scale, and the answer (X times Y) will be right below it on the bottom scale. For example, to figure out 3 times 2:

Move the '1' on the top scale to line up with the '2' on the bottom scale.
Look for the '3' on the top scale.
The answer, '6', will be directly below it on the bottom scale.

A slide rule set up to calculate 2 times X.

Sometimes, the number you need might go "off the scale." For example, if you want to find 2 times 7, and the '7' on the top scale doesn't line up with anything on the bottom scale. In these cases, you can slide the top scale to the left until its right end (also marked '1') lines up with the '2' on the bottom scale. This is like multiplying by 0.2 instead of 2.

A slide rule set up to calculate 0.2 times X.

If you do this, you must remember to move the decimal point in your final answer. If you calculated 0.2 times 7 and got 1.4, the real answer for 2 times 7 is 14. There are other ways to handle numbers going off the scale, like using different scales on the slide rule.

Dividing Numbers

Division is like the opposite of multiplication. The illustration below shows how to calculate 5.5 divided by 2:

Line up the '2' on the top scale with the '5.5' on the bottom scale.
Look for the '1' on the top scale.
The answer, '2.75', will be right below it on the bottom scale.

A slide rule set up to calculate X divided by 5.5.

This method for division is good because the final answer will never go off the scale.

Other Math Operations

Besides basic multiplication and division, many slide rules have other scales for different math functions. These often include:

Trigonometry: For finding sines and tangents (math about angles and triangles).
Logarithms: For finding the logarithm of a number.
Exponentials: For calculating numbers raised to a power (like e^x).

Some rules even have special scales for things like the Pythagorean theorem (for triangle sides) or for working with circles. The scales on linear slide rules are usually set up in a very standard way.

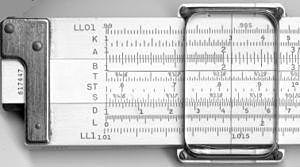
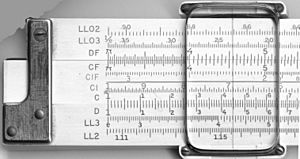
A, B	These are two-decade scales, good for finding square roots and squares of numbers.
C, D	These are single-decade scales, used for basic multiplication and division.
K	This is a three-decade scale, used for finding cube roots and cubes of numbers.
CF, DF	These are "folded" versions of C and D scales. They start from π (pi) instead of 1. This helps when your answer might be close to 10, or when you need to multiply or divide by π.
CI, DI, DIF	These are "inverted" scales, meaning they run from right to left. They help with calculations like 1 divided by X.
S	Used for finding sines and cosines on the D scale.
T	Used for finding tangents and cotangents on the D and DI scales.
ST, SRT	Used for sines and tangents of small angles and changing degrees to radians.
L	A straight scale used with C and D scales to find base-10 logarithms and powers of 10.
LLn	A set of log-log scales, used for finding logarithms and exponentials of numbers.
Ln	A straight scale used with C and D scales to find natural logarithms (base e) and e^x.

A slide rule designed to calculate 2 x X

A slide rule designed to calculate 0.2 x X

The scales on the front and back of a K&E 4081-3 slide rule.

Roots and Powers

To find the square of a number (X²), find X on the D scale and read its square on the A scale. To find a square root, do the opposite. The same applies for cubes and cube roots using the K scale. You need to be careful if a number appears in more than one place on a scale.

For problems like X^Y, you use the LL scales. You line up the '1' on the C scale with X on the LL scale. Then, find Y on the C scale, and the answer will be on the LL scale below it.

Trigonometry

The S, T, and ST scales are used for trigonometric functions (like sine and tangent) for angles in degrees. Many slide rules show angles in degrees and minutes. Some "decitrig" models use decimal parts of degrees instead.

Logarithms and Exponentials

You find base-10 logarithms and exponentials using the L scale, which is a straight scale. Some slide rules also have an Ln scale for natural logarithms (base e).

Addition and Subtraction

Slide rules are not usually used for addition and subtraction. However, there are two ways to do it if needed. One way involves changing the problem into a division problem. For example, to add X and Y, you can calculate (X divided by Y + 1) times Y.

The second method uses a sliding L scale found on some models. You slide the cursor left for subtraction or right for addition, then move the slide back to 0 to see the result.

Types of Slide Rules

Standard Linear Rules

The size of a slide rule is based on the length of its scales. Common "10-inch" models actually have scales that are 25 cm long, as they were made to metric standards. Smaller "pocket rules" are typically 5 inches long. Very large ones, a couple of meters long, were made for classrooms to help teach.

Usually, the marks on a slide rule let you read numbers with about two significant figures (digits that matter). You then guess the third digit. Some fancy slide rules have magnifying cursors to help you see the markings better, which can double the accuracy.

Many slide rules had helpful features. Trigonometric scales sometimes had two sets of labels, in black and red, for complementary angles. Duplex slide rules often had copies of some scales on the back. Scales were sometimes "split" to allow for greater accuracy.

Special slide rules were made for different types of engineering, business, and banking. These often had special scales for common calculations, like loan payments or finding the best amount to buy.

Circular Slide Rules

A Pickett circular slide rule with two cursors. (4.25 in./10.9 cm diameter) The back has an extra scale and one cursor.

A simple circular slide rule made by Concise Co., Ltd., Tokyo, Japan. It has scales for inverse, square, and cubic numbers. The back lists 38 metric/imperial conversion factors.

A Breitling Navitimer wristwatch with a circular slide rule built in.

Circular slide rules come in two main types. One has two cursors, and the other has a movable disk with a single cursor. The two-cursor type works by keeping a set angle between the cursors as you spin them around the dial for multiplication and division. The single-cursor type works more like a straight slide rule, by lining up the scales.

A big benefit of circular slide rules is that they are much smaller. A 10 cm circular rule can have the same accuracy as a 30 cm straight rule. Circular slide rules also avoid the problem of numbers going "off-scale" because the scales wrap around in a circle.

Circular slide rules are often stronger and move more smoothly. However, their accuracy depends on how well the central pivot is centered. Even a tiny error in the pivot can cause mistakes. The most accurate scales are usually on the outer rings. For more complex math, high-end circular rules might use spiral scales.

The main downsides of circular slide rules are that it can be harder to find numbers on a spinning disk, and they usually have fewer scales. Also, less important scales are closer to the center, which means they are less accurate. Most students learned on straight slide rules and didn't see a reason to switch.

One circular slide rule still used today is the E6B. This was first made in the 1930s for aircraft pilots to help them with dead reckoning (navigating without landmarks). It also helps with things like converting time, distance, speed, and temperature. Even though GPS and handheld calculators are common now, the E6B is still widely used as a main or backup tool, and many flight schools require students to learn how to use it.

In 1952, the Swiss watch company Breitling made a pilot's wristwatch with a built-in circular slide rule called the Breitling Navitimer. This watch could help with calculations for airspeed, climb/descent rates, flight time, distance, and fuel use.

Materials Used

In the past, slide rules were made from hard woods like mahogany or boxwood, with glass and metal cursors. Some very precise ones were even made of steel.

In 1895, a Japanese company, Hemmi, started making slide rules from bamboo. Bamboo was good because it stayed the same size, was strong, and was naturally smooth. The scales were made of celluloid or plastic. Later, slide rules were made entirely of plastic or aluminum painted with plastic. Modern cursors were made of acrylics or polycarbonates and slid on Teflon parts.

High-quality slide rules had numbers and scales carved into them and then filled with paint. Slide rules that were just painted or printed were seen as less good because the markings could wear off. However, Pickett, a very successful American slide rule company, made all its scales printed. Good slide rules also had clever catches to prevent them from falling apart and bumpers to protect the scales.

History of the Slide Rule

William Oughtred (1575–1660), who invented the circular slide rule.

The slide rule was invented around 1620–1630, soon after John Napier introduced the idea of logarithms. Edmund Gunter of Oxford created a tool with a single logarithmic scale that could be used for multiplication and division. In 1630, William Oughtred of Cambridge invented a circular slide rule. In 1632, he put two Gunter rules together to create something that looks like the modern slide rule.

In 1677, Henry Coggeshall made a two-foot folding rule for measuring timber, called the Coggeshall slide rule. This showed that slide rules could be useful for practical jobs, not just for math studies.

In 1815, Peter Mark Roget invented the log-log slide rule. This new scale helped users directly calculate roots and exponents, which was very useful for fractional powers.

Modern Design

The slide rule's more modern design was created in 1859 by a French army officer named Amédée Mannheim. Around this time, as engineering became a recognized job, slide rules became widely used in Europe. They became common in the United States after 1881. The duplex rule, which has scales on both sides, was invented in 1891 by William Cox.

During World War II, bombardiers and navigators used special slide rules for quick calculations. The U.S. Navy even designed a basic slide rule frame where different plastic cards could be inserted for specific calculations. This was used for aircraft range, fuel use, and altitude, and later for many other things.

An engineer using a slide rule. You can see a mechanical calculator in the background.

In the 1950s and 1960s, the slide rule was a symbol of the engineering profession. German rocket scientist Wernher von Braun used his old Nestler slide rules for his entire life, even when working on the American space program. Aluminum Pickett-brand slide rules were even carried on five Apollo space missions, including trips to the moon!

Many engineering students and engineers carried 10-inch slide rules in special belt holsters. Even in the mid-1970s, this was a common sight on college campuses. Students might also have a larger rule for precise work at home and a smaller pocket slide rule to carry around.

Why Slide Rules Declined

The importance of the slide rule began to fade as electronic computers became more available in the 1960s. The Fortran programming language (1957) made computers practical for solving math problems. Companies like IBM introduced more affordable computers for science and engineering. The BASIC programming language (1964) made computers easier for students to use.

Computers also changed how calculations were done. With slide rules, people focused on simplifying math problems to make them easier to solve. With computers, complex formulas could be typed in directly.

The final blow for the slide rule was the invention of pocket-sized scientific calculators. The 1972 Hewlett-Packard HP-35 was the first of these. These calculators could do most or all the functions of a slide rule. While they were expensive at first, by 1975, basic electronic calculators cost less than $50. By 1976, the TI-30 scientific calculator cost under $25. After this, the demand for slide rules quickly disappeared.

A TI-30 calculator.

Benefits of Slide Rules

Focus on important numbers: A slide rule usually gives answers with about three accurate digits. This matches most real-world data used in engineering. Modern calculators show many more decimal places, but the answer can't be more accurate than the numbers you put in.
Estimating size: A slide rule makes you constantly think about the size of your answer. For example, 1.5 × 30 (which is 45) looks the same on a slide rule as 1,500,000 × 0.03 (which is 45,000). You have to decide where the decimal point goes, which helps you understand the numbers better.
Quick checks: If you need to multiply or divide by the same number many times, you can often get the answer just by looking at the slide rule without moving it much. This is useful for things like calculating percentages or comparing prices.
No power needed: A slide rule does not need electricity to work.
Easy to make: You can build a slide rule from simple materials if you have an example to copy.
Standardized: All slide rules are very similar, so once you learn one, you can use any other.
Durable: Slide rules can be used in situations where it's hard to press small buttons, like when wearing gloves. They are less likely to have errors from accidentally pressing the wrong button.
Simple materials: Slide rules can even be made from cardboard or paper. Many free charts or special calculating tools made of cardboard are actually simple slide rules.

Using a slide rule along with an electronic calculator can be helpful. You can do an important calculation on both to double-check your work. Since they are so different, you are less likely to make the same mistake twice.

Downsides of Slide Rules

Mechanical errors: Mistakes can happen because of small imperfections in the way the slide rule is made.
Limited accuracy: Calculations on a slide rule are not perfectly precise because they use physical measurements. Modern calculators, however, can show answers with at least six accurate digits.

Images for kids

A homemade slide rule for teaching about base 2 numbers.
Quadratic and reciprocal scales.
A 7-foot teaching slide rule next to a normal-sized one.
A 1951 advertisement for an IBM computer, comparing it to engineers using slide rules.
A Faber-Castell slide rule with its pouch.
A very large slide rule on display at the MIT Museum.
A Fuller calculator from 1928.
An Otis King Model K slide rule.
A Bygrave slide rule.
A Thacher slide rule from around 1890.
An E6-B aviation computer.
A John Rabone & Sons cattle gauge from 1892.
Hurter and Driffield's actinograph.
A cryptographic slide rule used by the Swiss Army between 1914 and 1940.