Nested radical facts for kids

A nested radical is a mathematical expression where a root (like a square root) has another root inside it. Think of it like a set of Russian nesting dolls, but with numbers and roots!

For example, 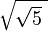is a nested radical because there's a square root of 5 inside another square root. Another example is 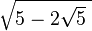, where the number 5 minus two times the square root of 5 is all under a larger square root.

What is a Nested Radical?

In algebra, a radical is just another name for a root, like a square root (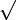Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{}\ ) or a cube root (Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt[3]{}\ ). When we say a radical is "nested," it means one radical sign is wrapped around another one. It's like a mathematical sandwich!

• Outer radical: This is the main root sign you see first.
• Inner radical: This is the root sign that is hidden inside the outer one.

These expressions might look a bit complicated at first, but they are just numbers written in a special way.

Why are they "Nested"?

They are called "nested" because one root is literally inside another. Imagine you have a box, and inside that box, there's another smaller box. In math, the outer radical is the big box, and the inner radical is the smaller box inside it.

For example, in 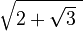Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{2+\sqrt{3}\ } :

• The outer radical is the big square root sign covering everything.
• The inner radical is 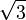Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{3}\ , which is inside the outer one.

Mathematicians often try to simplify these nested radicals to make them easier to work with. Sometimes, a nested radical can be rewritten without any nesting at all!

Simplifying Nested Radicals

Sometimes, a nested radical can be simplified into a form that doesn't have a root inside another root. This is often done using special formulas or by recognizing patterns.

One common formula for simplifying nested square roots looks like this: 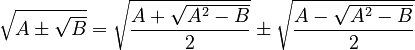Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{A \pm \sqrt{B}} = \sqrt{\frac{A+\sqrt{A^2-B}}{2}} \pm \sqrt{\frac{A-\sqrt{A^2-B}}{2}}

This formula works if 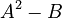Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A^2-B is a perfect square. If it is, then the nested radical can be "un-nested" into a simpler form, often as a sum or difference of two simpler square roots.

Example of Simplification

Let's look at an example to see how this works. Consider the nested radical 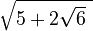Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{5+2\sqrt{6}\ } . This can be rewritten as Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{5+\sqrt{24}\ } (since Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2\sqrt{6} = \sqrt{4 \times 6} = \sqrt{24} ). Here, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A=5 and Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): B=24 . Let's check if Failed to parse (Missing <code>texvc</code> executable. 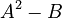Please see math/README to configure.): A^2-B is a perfect square: 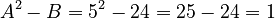Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A^2-B = 5^2 - 24 = 25 - 24 = 1 . Since 1 is a perfect square (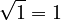Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{1}=1 ), we can simplify it!

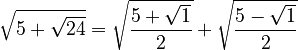
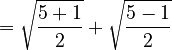
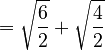
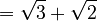
Using the formula: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{5+\sqrt{24}} = \sqrt{\frac{5+\sqrt{1}}{2}} + \sqrt{\frac{5-\sqrt{1}}{2}} Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): = \sqrt{\frac{5+1}{2}} + \sqrt{\frac{5-1}{2}} Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): = \sqrt{\frac{6}{2}} + \sqrt{\frac{4}{2}} Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): = \sqrt{3} + \sqrt{2}

So, the nested radical 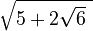Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{5+2\sqrt{6}\ } simplifies to 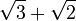Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{3} + \sqrt{2} . This is much easier to understand and use!

When are Nested Radicals Used?

Nested radicals appear in various areas of mathematics. They can show up when solving certain types of equations, especially those involving quadratic formulas or polynomials. They are also found in geometry when calculating lengths or distances in complex shapes.

While they might seem like a tricky part of algebra, understanding nested radicals helps you see how different parts of math connect and how complex expressions can sometimes be simplified into more manageable forms. It's like finding a hidden shortcut in a maze!

Images for kids

• 

  A friendly robot to guide you!

See also

• Square root
• Algebra
• In Spanish: Radical jerarquizado para niños