Partial fraction decomposition facts for kids
Partial fraction decomposition is a cool math trick! Imagine you have a big, complicated fraction, like one where the top and bottom parts are made of algebra expressions (like `x`s and numbers). This trick helps you break that big fraction down into several smaller, simpler fractions that are easier to work with. It's like taking a big LEGO model and splitting it back into smaller, easier-to-handle pieces.
In math, we're changing a fraction that looks like this: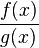 
Into a sum of smaller fractions that look like this: 
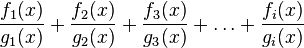The bottom parts (denominators) of all these smaller fractions are special. They are factors of the original big fraction's bottom part, `g(x)`. This means if you multiply all the `g_i(x)` parts together, you would get `g(x)`.
Contents
What Is Partial Fraction Decomposition?
Partial fraction decomposition is a method used in algebra to rewrite a rational function (which is just a fancy name for a fraction where the top and bottom are polynomials) as a sum of simpler fractions. Think of it like reversing the process of adding fractions. When you add fractions, you find a common denominator. This method goes the other way: it takes a fraction and breaks it into the pieces that would have been added together.
For example, if you had the fraction: 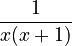Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{x(x+1)} Partial fraction decomposition would help you see that it's the same as: 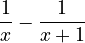Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{x} - \frac{1}{x+1} See how the original denominator `x(x+1)` is made up of the denominators `x` and `x+1` from the simpler fractions?
Why Do We Use This Math Trick?
This method is super useful in higher-level math, especially in calculus. One of the main reasons we use partial fractions is to find the antiderivatives of algebra fractions. An antiderivative is like the opposite of a derivative; it's a way to "undo" differentiation.
Imagine you have a complicated fraction and you need to find its antiderivative. It might be very hard to do directly. But if you break it down into simpler fractions using partial decomposition, finding the antiderivative for each smaller piece becomes much easier. Then, you just add up the antiderivatives of the simpler pieces.
How Does It Work?
The basic idea is to take a fraction like 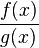and assume it can be written as a sum of simpler fractions. The type of simpler fractions you get depends on the factors of the denominator `g(x)`.
Simple Factors
If `g(x)` has simple factors like `(x-a)`, then for each `(x-a)` factor, you'll have a fraction like 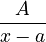Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{A}{x-a} . Here, `A` is just a number we need to figure out.
Repeated Factors
If `g(x)` has a factor like `(x-a)^2` (meaning `(x-a)` appears twice), then you'll need fractions for each power up to the highest one. So, for `(x-a)^2`, you'd have 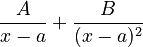Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{A}{x-a} + \frac{B}{(x-a)^2} .
Quadratic Factors
Sometimes, `g(x)` might have factors that are quadratic (like `x^2+bx+c`) and can't be broken down further into simpler `(x-a)` factors using real numbers. For these, the top part of the fraction will be a linear expression, like 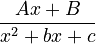Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{Ax+B}{x^2+bx+c} .
After setting up these simpler fractions with unknown numbers (like A, B, C), you then solve a system of equations to find what those numbers are. Once you have the numbers, you've successfully decomposed the original fraction!
See also
In Spanish: Descomposición en fracciones simples para niños
