Rational function facts for kids

A rational function is a special type of function in mathematics. It's made by dividing one polynomial by another polynomial. Think of it like a fraction, but instead of numbers, you have expressions with variables (like 'x') and powers.

For example, f(x) = x/x − 3 is a rational function. Here, 'x' is a polynomial, and 'x - 3' is another polynomial.

An asymptote is a line that a curve gets closer and closer to touching but never actually touches. Imagine a car driving towards a wall, getting closer and closer, but never quite hitting it. That's how a curve behaves near an asymptote. These lines help us understand the shape and behavior of rational functions.

This image shows a rational function. The dotted lines are the asymptotes, which the curve gets very close to but never touches.

What is a Rational Function?

A rational function is a fraction where the top part (the numerator) and the bottom part (the denominator) are both polynomials. A polynomial is an expression that can have variables, coefficients, and exponents, like x² + 3x - 2.

How to Spot a Rational Function

• It must be written as a fraction.
• The top part must be a polynomial.
• The bottom part must also be a polynomial.
• The bottom part cannot be zero. If the denominator is zero, the function is undefined at that point.

Examples of Rational Functions

• f(x) = 1/x
• g(x) = x + 2/x - 1
• h(x) = x² + 3x - 2/x² - 4

These functions are important in many areas, including physics, engineering, and economics, to describe things like how quickly something cools down or how much a population grows.

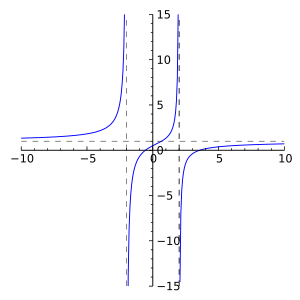
Understanding Asymptotes

Asymptotes are imaginary lines that guide the shape of a rational function's graph. The graph of the function gets closer and closer to these lines as it moves further away from the center, but it never actually crosses or touches them.

This graph shows a curve getting closer to the red line (an asymptote) without ever touching it.

Types of Asymptotes

There are three main types of asymptotes you might see with rational functions:

• Vertical Asymptotes: These are vertical lines (up and down). They happen when the denominator of the rational function becomes zero. For example, in f(x) = 1/x, the vertical asymptote is at x = 0 because you can't divide by zero.
• Horizontal Asymptotes: These are horizontal lines (left and right). They describe what happens to the function's value as 'x' gets very, very large (either positive or negative).
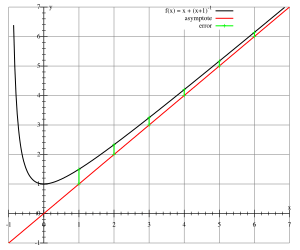
• Slant (or Oblique) Asymptotes: These are diagonal lines. They appear when the degree (the highest power of 'x') of the numerator is exactly one more than the degree of the denominator.

Why Asymptotes Are Important

Asymptotes help us understand the behavior of a function, especially when 'x' gets very large or when the function is undefined. They show us the limits of the function and how its graph will look. They are like invisible boundaries that the function's graph approaches but never crosses.

See also

• In Spanish: Función racional para niños

Images for kids

• 

  A friendly robot, ready to learn!