Piecewise facts for kids
A piecewise function is a special kind of math rule that uses different formulas for different parts of its input numbers. Imagine you have a game, and the rules change depending on which part of the game board you are on. That's similar to how a piecewise function works! It uses different math formulas for different parts of its domain, which are all the possible numbers you can put into the function.
These different rules are often grouped together using a big curly bracket, like this: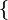 
. For example, a function might give you `2x` when `x` is greater than 0, but `x-1` when `x` is 0 or less.
What is a Piecewise Function?
A piecewise function is a function that is defined by multiple rules or formulas. Each rule applies to a specific part of the function's domain. The domain is simply the set of all possible input values for the function.
Think of it like a set of instructions. If your input number is in one group, you follow one instruction. If it's in another group, you follow a different instruction. All these instructions together make up the single piecewise function.
How Does It Work?
Let's look at an example to understand this better. Imagine a function named `f(x)`. It could be defined like this:
- If `x` is greater than 0 (meaning `x > 0`), then `f(x)` equals `2x`.
- If `x` is 0 or less (meaning `x ≤ 0`), then `f(x)` equals `x - 1`.
So, if you want to find `f(5)`:
- Since 5 is greater than 0, you use the first rule: `f(5) = 2 * 5 = 10`.
And if you want to find `f(-2)`:
- Since -2 is less than 0, you use the second rule: `f(-2) = -2 - 1 = -3`.
The big curly bracket 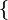is used to show that all these different rules belong to the same function.
Common Examples
Some functions you might already know are actually piecewise functions, even if they aren't always called that directly.
- Absolute Value Function: The absolute value function `|x|` gives you the positive version of any number.
* If `x` is greater than or equal to 0, `|x|` is just `x`. * If `x` is less than 0, `|x|` is `-x` (which makes it positive). This is a perfect example of a piecewise function.
- Floor Function: The floor function `floor(x)` gives you the largest whole number that is less than or equal to `x`. For example, `floor(3.7)` is 3, and `floor(-2.1)` is -3. This function changes its rule at every whole number.
- Step Function: A step function looks like steps on a graph. It stays constant for a while and then suddenly jumps to a new value. These jumps happen at specific points, making it a piecewise function.
See also
In Spanish: Función definida a trozos para niños
