Pizza theorem facts for kids
The pizza theorem is a cool idea in geometry that talks about cutting a circle (like a pizza!) in a special way. It shows that two people can get the same amount of pizza.
It's called the pizza theorem because it's like sharing a pizza. If you slice a pizza into 8 pieces (or 12, 16, etc.), and two friends take turns picking slices, they'll both end up with the same amount of pizza. This is true even if the cuts don't meet exactly in the middle of the pizza!
Contents
How the Pizza Theorem Works
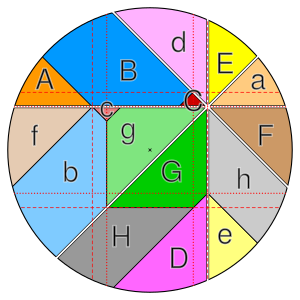
Imagine a point p inside a circle. Now, imagine you cut the circle into n slices, where n is a number like 8, 12, 16, and so on. This number n must be a multiple of 4.
You make these slices by drawing lines through point p. Each slice will have the same angle. If you number the slices around the pizza (1, 2, 3, 4, etc.), the pizza theorem says:
- The total area of all the odd-numbered slices (1, 3, 5, etc.) is exactly the same as the total area of all the even-numbered slices (2, 4, 6, etc.).
This means if two people take turns picking slices, one taking all the odd slices and the other taking all the even slices, they will each get an equal amount of pizza!
Who Discovered the Pizza Theorem?
The idea for the pizza theorem first appeared as a challenge problem in 1967. A person named Michael Goldberg later published a solution to this problem.
Later, in 1994, mathematicians Carter and Wagon found a different way to prove the theorem. They showed how you could cut the pizza slices into smaller pieces and rearrange them. This rearrangement would show that the odd-numbered pieces and the even-numbered pieces are exactly the same size. More proofs using this "dissection" method have been found since then.
When the Theorem Works (and When It Doesn't)
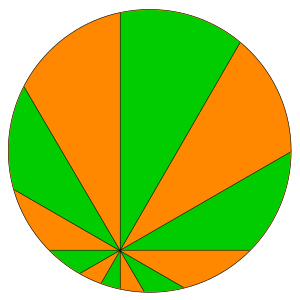
The rule that the number of slices must be a multiple of four (like 8, 12, 16) is very important. If you cut a pizza into a number of slices that is not a multiple of four, the areas might not be equal.
For example, if you cut a pizza into 4 slices, or 6 slices, the two people might not get equal amounts.
- If you cut the pizza into 2, 10, 18, etc., slices (numbers that are 2 more than a multiple of 8), the person whose slices include the center point of the pizza will get less pizza.
- If you cut the pizza into 6, 14, 22, etc., slices (numbers that are 6 more than a multiple of 8), the person whose slices include the center point will get more pizza.
However, if any of your cuts go exactly through the very center of the pizza, then both people will always get an equal share, no matter how many slices there are.
Crust and Toppings Too!
When the pizza is divided equally by area, something cool happens: the crust is also divided equally! This means the edge of the pizza, or any toppings that are spread in a circle (like pepperoni or cheese), will also be split fairly. This works as long as the toppings are within a circle that includes the point p where you made your cuts.
But, if the pizza is divided unevenly (when the number of slices isn't a multiple of 4), the person who gets more pizza area actually gets less crust!
Sharing with More People
The pizza theorem can also help share pizza with more than two people. If a pizza is cut into a number of slices that is a multiple of four (like 8, 12, 16), it can be shared equally among n/4 people. For example, a pizza cut into 12 slices can be shared equally by three people (12 divided by 4 equals 3).
Mathematicians also study games about choosing pizza slices. Imagine a pizza cut into slices, but not necessarily equal ones. Two people take turns picking slices that are next to ones already eaten. If both people try to get the most pizza, the person who takes the first slice can guarantee they get at least 4/9 of the whole pizza.
This is part of a bigger idea called "fair division." It looks at how to share things when different people might value different parts of it. For example, one person might want the most pepperoni, while another wants the most cheese!
Beyond Flat Pizzas
There's a similar idea to the pizza theorem for objects in higher dimensions, not just flat circles. It's about how volumes are divided.
This is a bit like the ham sandwich theorem. That theorem says that you can always make one straight cut through any ham sandwich (no matter how lumpy!) to divide the bread, ham, and cheese all exactly in half at the same time. For a 2D pizza, it means one straight cut can divide both the area and the crust length in half.
See also
 In Spanish: Teorema de la pizza para niños
In Spanish: Teorema de la pizza para niños