Polar moment of inertia facts for kids

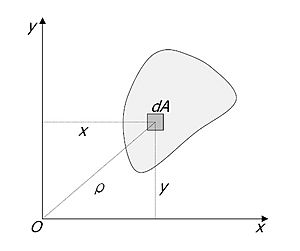
The polar second moment of area is a way to measure how well an object's shape resists twisting. Think of it like this: some shapes are better at stopping a twisting force (called torsion) than others.

This idea is part of a bigger topic called the Second moment of area. While the regular second moment of area helps engineers figure out how much a beam will bend, the polar second moment of area tells them how much something will twist.

You'll often see the polar second moment of area called J or I_z in engineering books. It's super important for designing things that twist, like the axles or drive shafts in a car. These parts need to be strong enough to handle twisting forces without breaking or deforming too much.

The polar second moment of area is usually measured in units like meters to the fourth power (m⁴) or inches to the fourth power (in⁴).

How it Works

Imagine you have a shape. The polar second moment of area is calculated based on how far away each tiny part of that shape is from the center of the twist. The further away the material is from the center, the more it helps resist twisting.

A diagram showing how the polar second moment of area is calculated for a shape. ρ is the distance from the center of twist.

For simple shapes, especially round ones like a solid or hollow cylinder, the calculations are pretty straightforward. If a shape isn't round, like a square beam, it can warp when twisted. In those cases, engineers use a special "torsional constant" to make the calculations more accurate.

Twisting and Resistance

The bigger the polar second moment of area (J) of an object, the more twisting force (called torque) you'll need to make it twist. This means the object's shape makes it strong against twisting.

But it's not just about the shape! The material an object is made from also matters. Some materials are naturally stiffer and resist twisting better than others. This material stiffness is called the Shear modulus, and it's usually shown as G.

Engineers use both the shape's resistance (J) and the material's resistance (G) to figure out how much an object will twist. They use this formula:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \theta = \frac{Tl}{JG}

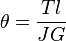
Let's break down what each letter means:

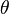• (theta) is the angle the object twists.
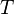• is the twisting force (torque) applied.
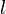• is the length of the object.
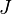• is the polar second moment of area (how the shape resists twisting).
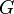• is the shear modulus (how the material resists twisting).

So, if you apply a lot of twisting force (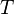) or have a very long object (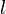), it will twist more. But if the object has a large J (a shape that resists twisting well) or is made of a material with a high G (a stiff material), it will twist less.

Related pages

• Moment (physics)
• Second moment of area
• List of second moments of area for standard shapes
• Shear modulus

Images for kids

• 

  The rotor of a modern steam turbine. This part needs to resist twisting forces.