Nth root facts for kids

Pascal's Triangle showing P(4,1) = 4.

The nth root of a number is like solving a puzzle. You are looking for a number that, when multiplied by itself a certain number of times, gives you the original number. Imagine you have a number, let's call it r. The nth root of r is a number, let's call it k, that makes this true:

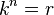
Here, 'n' tells you how many times k is multiplied by itself. For example, if n is 2, you multiply k by itself 2 times (k × k). If n is 3, you multiply k by itself 3 times (k × k × k).

We write the nth root using a special symbol: . The little 'n' above the root symbol is called the index, and r (the number inside) is called the radicand.

What is an Nth Root?

An nth root helps us find a base number when we know the result of it being multiplied by itself many times. It's the opposite of exponentiation. For example, if you know that 3 multiplied by itself 2 times (3 x 3) equals 9, then the 2nd root (or square root) of 9 is 3.

Understanding the Index 'n'

The index 'n' tells you which root you are looking for.

• If n = 2, it's a square root.
• If n = 3, it's a cube root.
• If n = 4, it's a fourth root, and so on.

When 'n' is 2 (for a square root), we usually don't write the '2' above the root symbol. So, 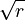Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{r} means the square root of r.

Examples of Nth Roots

Let's look at some common examples to make this clearer.

Square Roots

The square root of a number is the value that, when multiplied by itself, gives the original number.

• The square root of 25 is 5, because 5 × 5 = 25. We write this as Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{25} = 5 .
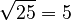• The square root of 100 is 10, because 10 × 10 = 100. We write this as Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{100} = 10 .

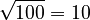Square roots are often used when working with areas of squares. If a square has an area of 36 square units, its side length is 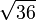Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{36} , which is 6 units.

Cube Roots

The cube root of a number is the value that, when multiplied by itself three times, gives the original number.

• The cube root of 8 is 2, because 2 × 2 × 2 = 8. We write this as Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt[3]{8} = 2 .
• The cube root of 64 is 4, because 4 × 4 × 4 = 64. We write this as Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt[3]{64} = 4 .

Cube roots are useful when dealing with the volume of cubes. If a cube has a volume of 27 cubic units, its side length is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt[3]{27} , which is 3 units.

Why Are Nth Roots Important?

Nth roots are not just for math class; they are used in many real-world situations.

• Geometry: Finding the side lengths of squares or cubes when you know their area or volume.
• Engineering: Calculating sizes or strengths in designs.
• Finance: Understanding growth rates over time.
• Science: Solving problems in physics and chemistry.

They help us reverse calculations and find missing pieces of information in various problems.

See also

In Spanish: Radicación para niños