Statistical parameter facts for kids
A statistical parameter (also called a population parameter) is a special number that helps describe a whole group of things, like all the students in a school or all the trees in a forest. It's a fixed value that tells us something important about a statistical population or a statistical model.
Imagine you want to know the average height of all 12-year-olds in your country. This "average height" for everyone would be a statistical parameter. It's a true value that exists for the entire group.
Contents
What is a Statistical Parameter?
A statistical parameter is a number that describes a feature of a large group, called a population. This number is usually unknown because it's impossible to measure every single thing in a huge group.
For example:
- The average age of all people living in a city.
- The percentage of all students in a school who like pizza.
- The typical weight of all apples grown in an orchard.
These numbers are fixed for that specific population. They don't change unless the population itself changes.
Why are Parameters Important?
Parameters are super important in statistics because they help us understand big groups without having to check every single member. Even though we usually don't know the exact value of a parameter, we try to guess it using information from smaller groups.
Knowing about parameters helps scientists, researchers, and even governments make smart decisions. For instance, if you know the average income of a city, you can plan better for schools or hospitals.
Parameters vs. Estimators
It's easy to confuse a statistical parameter with an estimator. They are related but different:
- A parameter is the true, fixed number that describes the entire population. We often use the Greek letter
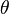(pronounced "theta") to stand for a parameter. - An estimator is a guess or an estimate of that parameter. We get this guess by looking at a smaller part of the population, called a sample. The value of an estimator can change each time you take a different sample. We often use
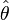(pronounced "theta-hat") for an estimator.
Think of it this way:
- The parameter is the exact average height of all students in your school (a fixed number).
- An estimator would be the average height of just your class (a guess based on a smaller group). If you picked a different class, you might get a slightly different average height.
So, while the parameter is a fixed, true value for the whole group, the estimator is a changing value that tries to get close to that true value using limited information.
Related pages
