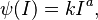Stevens's power law facts for kids
Stevens' power law helps us understand how our senses work. It's a scientific idea in psychophysics, which is the study of how physical things (like light or sound) connect to what we feel and sense. This law explains that when a physical stimulus, like a bright light or a loud sound, gets stronger, the feeling or sensation we have from it also gets stronger in a predictable way.
This idea is named after a scientist named Stanley Smith Stevens (1906–1973). Even though some people had similar ideas before, Stevens brought this "power law" back into focus. He published a lot of data in 1957 to show that it was true for many different senses.
The basic idea of the law can be shown with a math formula:
Don't worry, it's simpler than it looks!
- I stands for the strength of the physical stimulus. This could be how bright a light is, how heavy something feels, or how loud a sound is.
- ψ(I) (pronounced "psi of I") stands for how strong the sensation feels to you.
- a is a special number called an "exponent." This number changes depending on what sense we are talking about. For example, the a for how loud something sounds is different from the a for how bright something looks.
- k is just a constant number that helps the math work out, depending on the units used.
This law is often seen as an improvement over an older idea called the Weber–Fechner law. That's because Stevens' power law can describe how we sense things even when the stimulus is very weak, almost zero.
The table below shows some of the "exponent" numbers (a) that Stevens found for different senses:
| Sense | Exponent (a) | What was being sensed |
|---|---|---|
| Loudness | 0.67 | How loud a 3000 Hz sound was |
| Vibration | 0.95 | How strong a 60 Hz vibration felt on a finger |
| Vibration | 0.6 | How strong a 250 Hz vibration felt on a finger |
| Brightness | 0.33 | A small light in the dark |
| Brightness | 0.5 | A single point of light |
| Brightness | 0.5 | A quick flash of light |
| Brightness | 1 | A single point of light flashed quickly |
| Lightness | 1.2 | How light or dark gray papers looked |
| Visual length | 1 | The length of a projected line |
| Visual area | 0.7 | The size of a projected square |
| Redness (saturation) | 1.7 | How red a red-gray mix looked |
| Taste | 1.3 | How sweet Sucrose tasted |
| Taste | 1.4 | How salty salt tasted |
| Taste | 0.8 | How sweet Saccharin tasted |
| Smell | 0.6 | The smell of Heptane |
| Cold | 1 | How cold a metal touch on the arm felt |
| Warmth | 1.6 | How warm a metal touch on the arm felt |
| Warmth | 1.3 | How warm a small area of skin felt from heat |
| Warmth | 0.7 | How warm a large area of skin felt from heat |
| Discomfort, cold | 1.7 | How uncomfortable whole-body cold felt |
| Discomfort, warm | 0.7 | How uncomfortable whole-body warmth felt |
| Thermal pain | 1 | Pain from heat on the skin |
| Tactual roughness | 1.5 | How rough rubbing emery cloths felt |
| Tactual hardness | 0.8 | How hard squeezing rubber felt |
| Finger span | 1.3 | The thickness of blocks felt by fingers |
| Pressure on palm | 1.1 | How much pressure felt on the skin |
| Muscle force | 1.7 | How strong muscle contractions felt |
| Heaviness | 1.45 | How heavy lifted weights felt |
| Viscosity | 0.42 | How thick stirring silicone fluids felt |
| Electric shock | 3.5 | The feeling of current through fingers |
| Vocal effort | 1.1 | How much effort felt when speaking |
| Angular acceleration | 1.4 | The feeling of 5 seconds of rotation |
| Duration | 1.1 | How long white-noise sounds felt |
Contents
How Scientists Measure Sensations
Stevens used a few main ways to figure out how strong people felt a stimulus.
Magnitude Estimation
Imagine a scientist shows you a light and says, "This light has a brightness of 10." Then they show you another light. If the second light seems twice as bright, you would say "20." If it seems half as bright, you would say "5." This is called magnitude estimation with a standard. You are comparing everything to the first "standard" light.
Sometimes, people just start by picking their own number for the first stimulus. Then they keep using numbers that show how much stronger or weaker the next sensations feel compared to the first. This is called magnitude estimation without a standard.
Magnitude Production
This is the opposite of estimation. A scientist might tell you, "Make a sound that is twice as loud as this first sound." You would then adjust a sound until it felt twice as loud to you.
Cross-Modality Matching
This method is really interesting! It's when you match one type of sensation to another. For example, a scientist might ask you to adjust the brightness of a light until it feels as strong as a certain amount of warmth or pressure. This helps scientists compare how different senses work.
Things People Questioned About the Law
Even though Stevens' power law is widely used, some scientists have raised questions about it.
One main point of discussion is that Stevens often averaged the data from many people. While this gave a good overall picture, it might hide the fact that each person senses things a little differently. What feels "twice as loud" to one person might not feel exactly "twice as loud" to another.
Another question is whether the way we measure sensations truly shows a perfect "ratio scale." This means if something feels twice as strong, is it truly twice as strong in a measurable way? Some studies have shown that people don't always interpret numbers in a perfectly exact way when judging sensations.
Also, the way we perceive things can change depending on the situation. For example, a sound might feel less loud if there's a lot of background noise. This means that our sensations aren't always "absolute" or fixed; they can be affected by what's happening around us.
See also
 In Spanish: Función potencial de Stevens para niños
In Spanish: Función potencial de Stevens para niños
- Perception
- Sone