String girdling Earth facts for kids
The String Girdling Earth is a fun math puzzle with a surprising answer. Imagine you have a string wrapped perfectly around the Earth's equator. Now, you cut the string and add just one meter (about 3 feet) to its length. If you then lift the entire string so it's at the same height all the way around, how big would the gap be between the string and the Earth? Would it be big enough for a car, a cat, or just a thin knife blade?
The Surprising Answer
Most people think that adding only one meter to a string that goes around the entire Earth (which is about 40,000 kilometers long!) wouldn't make much of a difference. They might guess the gap would be tiny, maybe just enough for a knife blade.
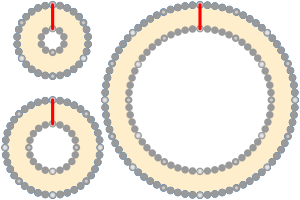
But here's the surprising part: the gap would actually be wide enough for a cat to walk through easily! The space created would be about 16 centimeters (or about 6 inches) all the way around.
Even more amazing is that the size of the original circle doesn't matter at all. Whether the string is around a tiny atom, a basketball, or even the huge Milky Way galaxy, adding one meter to its length will always create a gap of about 16 centimeters.
How Does It Work?
Let's think about circles. The distance around a circle is called its circumference. You can find the circumference using a simple math formula:
- Circumference = 2 × pi (π) × radius
Here, 'pi' (π) is a special number, approximately 3.14159. The 'radius' is the distance from the center of the circle to its edge.
When you add one meter to the string, you are increasing the circumference. Let's say the original Earth's radius is R. The new, slightly larger circle will have a new radius, let's call it R + r. The 'r' is the extra height the string is lifted.
The math shows that the extra height r is always equal to the added length (1 meter in our puzzle) divided by 2 times pi (2π).
So, if you add 1 meter to the string:
- Extra height (r) = 1 meter / (2 × π)
- Extra height (r) ≈ 1 meter / 6.28
- Extra height (r) ≈ 0.159 meters, which is about 16 centimeters!
This means that no matter how big the original circle is, if you add the same amount of length to its circumference, the string will always lift off the surface by the same amount.
Real-World Example
This idea also explains something you might have seen at an athletics track. On a running track, the starting lines for each lane are staggered. This is because the outer lanes are longer than the inner lanes. To make sure every runner runs the same distance, the starting points are moved forward for the outer lanes.
The difference in starting points between two lanes is always 2π times the width of the lane. So, if a lane is 1 meter wide, the starting line for the next lane will be about 6.28 meters (2π × 1 meter) ahead, no matter how big the entire track is!
See also
 In Spanish: Cuerda que rodea la Tierra para niños
In Spanish: Cuerda que rodea la Tierra para niños