16-cell facts for kids
A 16-cell is a special kind of shape that exists in four dimensions. Think of it like a 3D cube, but with an extra dimension! It's also called a hexadecachoron. This shape is one of six "perfect" 4D shapes, first described by a Swiss mathematician named Ludwig Schläfli in the mid-1800s.
The mathematician John Horton Conway also called it an orthoplex. This name helps describe a whole group of similar shapes called cross-polytopes.
Contents
What is a 16-Cell?
The 16-cell is part of a family of shapes called cross-polytopes, which can be found in any number of dimensions. Its "opposite" shape (called a dual) in four dimensions is the tesseract, which is like a 4D cube.
This amazing shape is made up of 16 smaller shapes called tetrahedra. A tetrahedron is a 3D shape with four triangular faces, like a pyramid with a triangle base.
The 16-cell has:
- 16 cells (each a tetrahedron)
- 32 triangular faces
- 24 edges (lines)
- 8 vertices (points or corners)
Imagine the 8 points of the 16-cell. They can be described using coordinates like (±1, 0, 0, 0) in four dimensions. All these points are connected by edges, except for points that are directly opposite each other.
How is it Built?
The Schläfli symbol for the 16-cell is {3,3,4}. This symbol is a special code that tells mathematicians how the shape is put together.
If you look at any single corner (vertex) of the 16-cell, you would see:
- 8 tetrahedra meeting there
- 12 triangles meeting there
- 6 edges meeting there
The shape formed by the points around any vertex is a regular octahedron. An octahedron is an 8-sided shape made of triangles.
If you look at any single edge of the 16-cell, you would see:
- 4 tetrahedra meeting there
- 4 triangles meeting there
The shape formed by the points around any edge is a square.
There's also a slightly different version of the 16-cell called a demitesseract or 4-demicube. It's part of the demihypercube family and can be thought of as having alternating colored tetrahedral cells.
Tiling 4D Space
Just like you can tile a floor with squares, you can also tile four-dimensional Euclidean space with regular 16-cells. This is called the hexadecachoric honeycomb. Its Schläfli symbol is {3,3,4,3}.
There are only three ways to perfectly tile 4D space with regular shapes:
- Using 16-cells (the hexadecachoric honeycomb)
- Using 24-cells (the icositetrachoric honeycomb)
- Using tesseracts (the tesseractic honeycomb)
In the hexadecachoric honeycomb, each 16-cell touches many others:
- 16 neighbors share a whole octahedron with it.
- 24 neighbors share only an edge with it.
- 72 neighbors share only a single point with it.
At any given point in this tiling, twenty-four 16-cells meet up.
Seeing the 16-Cell
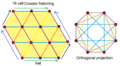
It's hard to imagine a 4D shape, so mathematicians use "projections" to see them in 3D space. Think of it like a shadow of the 4D shape.
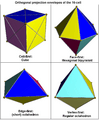
- Cell-first projection: If you project the 16-cell into 3D space by looking at it "cell-first," it looks like a cube. Inside this cube, you'd see two tetrahedra that fit perfectly. The other 14 cells of the 16-cell fill up the rest of the cube's space.
- Vertex-first projection: If you project the 16-cell by looking at it "vertex-first," it looks like an octahedron. The closest point of the 16-cell to you would appear right in the center of this octahedron.
Related Shapes
- 24-cell
- Polychoron
Images for kids
-
This image shows a "net" of the 16-cell, which is like unfolding it into 3D space.
-
These are different ways the 16-cell can be projected into 3D space, showing its "shadow" shapes.
See also
In Spanish: Hexadecacoron para niños
