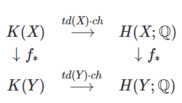Atiyah–Singer index theorem facts for kids
| Field | Differential geometry |
|---|---|
| First proof by | Michael Atiyah and Isadore Singer |
| First proof in | 1963 |
| Consequences | Chern–Gauss–Bonnet theorem Grothendieck–Riemann–Roch theorem Hirzebruch signature theorem Rokhlin's theorem |
The Atiyah–Singer index theorem is a big idea in differential geometry, a part of math that studies shapes and spaces. It was proven by two mathematicians, Michael Atiyah and Isadore Singer, in 1963.
This theorem connects two different ways of looking at special math tools called "elliptic differential operators" on shapes that are "compact manifolds" (think of a sphere or a donut, but in higher dimensions). One way is called the analytical index, which is about the number of solutions to certain equations. The other is the topological index, which is about the shape's properties. The theorem says these two numbers are always the same!
This theorem is very important because it brings together ideas from different areas of math. It also helps explain many other theorems, like the Chern–Gauss–Bonnet theorem and the Riemann–Roch theorem. It even has uses in theoretical physics.
Contents
History
The idea for the index theorem came from a mathematician named Israel Gel'fand. He noticed that the "index" of certain math problems didn't change even if the shape was stretched or bent, as long as it wasn't torn. He wondered if there was a formula for this index using only the shape's basic properties.
Other important ideas that led to the theorem included the Riemann–Roch theorem and the Hirzebruch signature theorem. In 1961, Atiyah and Singer rediscovered a special math tool called the Dirac operator. Atiyah thought that if this operator's "index" was always a whole number, it could explain some tricky math observations.
The Atiyah–Singer theorem was announced in 1963. Their first published proof used a math idea called K-theory. Later, in 1973, Atiyah, Raoul Bott, and Vijay Patodi found a new way to prove the theorem using the heat equation, which is a way to describe how heat spreads.
Over the years, many other mathematicians built on their work:
- In 1965, Sergey P. Novikov showed how certain properties of shapes, called Pontryagin classes, were always the same even if the shape was changed smoothly.
- In 1969, Michael Atiyah defined "abstract elliptic operators," which are like the original operators but can work on more general spaces.
- In 1971, Isadore Singer suggested many ways to expand the index theory even further.
- In 1984, Nicolae Teleman proved the index theorem for "topological manifolds," which are shapes that are not necessarily smooth. This showed that the theorem is really about the shape itself, not just how smooth it is.
- In 1986, Alain Connes introduced "noncommutative geometry," which is a new way to think about spaces, and the index theorem has been important there too.
What the Symbols Mean
To understand the theorem, we use some symbols:
- X is a compact and smooth manifold. Think of a compact manifold as a shape that is closed and doesn't have any edges, like the surface of a ball. "Smooth" means it doesn't have any sharp corners.
- E and F are "vector bundles" over X. These are like extra spaces attached to each point of X. Imagine a tiny arrow (a vector) sticking out of every point on a sphere.
- D is an "elliptic differential operator." This is a special kind of math rule that changes functions from E into functions in F.
Symbol of a Differential Operator
Imagine a math rule that uses derivatives, like finding how fast something changes. The "symbol" of this rule is a simpler version that only keeps the most important parts, the highest order terms.
For example, the Laplace operator is a rule that helps describe things like heat flow. Its symbol is like a squared distance. This operator is called elliptic because its symbol is never zero unless all the inputs are zero. This means it's "almost invertible," which is a key property.
If an operator is elliptic, it means it's very powerful. It has a "pseudoinverse," which is like an inverse but not quite perfect. This is important because it means the number of solutions to equations involving these operators is limited.
Analytical Index
For an elliptic operator D, the "analytical index" is a number that tells us something about its solutions. It's calculated by:
- Finding the number of solutions to the equation Df = 0. This is called the "kernel" of D.
- Finding the number of "constraints" on the right side of an equation like Df = g. This is called the "cokernel" of D.
The analytical index is the difference between these two numbers: Index(D) = (size of kernel of D) − (size of cokernel of D).
Even though the kernel and cokernel can change a lot, their *difference* (the index) changes smoothly. This is why the index can be described using the shape's properties.
Topological Index
The "topological index" is a number that describes the same elliptic operator, but it's calculated using the shape of the manifold and the vector bundles, not by solving equations. It uses ideas like the Todd class and the Chern character, which are ways to measure the "twistiness" or "complexity" of the shape and its attached bundles.
While the formula for the topological index looks complicated, it's usually easier to calculate than the analytical index.
The Atiyah–Singer index theorem states: The analytical index of D is equal to its topological index.
This means that a number found by solving complex equations (analytical index) is exactly the same as a number found by looking at the shape's properties (topological index). This is a very powerful connection! It helps mathematicians find the analytical index, which is usually very hard to get directly.
Also, the analytical index is always a whole number. The topological index, by its definition, might seem like it could be a fraction. But because the theorem says they are equal, it proves that the topological index must also always be a whole number, which is a deep discovery.
Relation to Grothendieck–Riemann–Roch
The Grothendieck–Riemann–Roch theorem was a big inspiration for the index theorem. It's another theorem that connects different math ideas. The Atiyah–Singer theorem is like a version of the Grothendieck–Riemann–Roch theorem for "real" shapes, not just complex ones.
Examples
The Atiyah–Singer index theorem helps prove many other important theorems. Here are a few:
Chern-Gauss-Bonnet Theorem
Imagine a compact, oriented manifold (a closed, smooth shape) in 2D, like the surface of a sphere. The Chern–Gauss–Bonnet theorem says that its Euler characteristic (a number that describes its shape, like 2 for a sphere) can be found by integrating its "Euler class" over the surface. The index theorem helps prove this by using a special operator related to how forms behave on the manifold.
Hirzebruch–Riemann–Roch Theorem
This theorem is for "complex manifolds," which are shapes that can be described using complex numbers. It connects the "holomorphic Euler characteristic" (a number related to solutions of certain equations on the complex manifold) to a topological formula involving the Chern character and Todd class of the manifold. The Atiyah–Singer index theorem provides a way to prove this.
Hirzebruch Signature Theorem
The Hirzebruch signature theorem is about the "signature" of a compact, oriented manifold. The signature is a number that tells us something about the shape's "twistiness" in higher dimensions. This theorem says the signature is equal to the "L genus" of the manifold, which is a topological property. The index theorem helps prove this by using a special "signature operator."
 Genus and Rochlin's Theorem
The  genus is another number that describes a manifold. For special shapes called "spin manifolds," the  genus is always a whole number. The index theorem shows that the  genus for spin manifolds is the index of a Dirac operator.
In 4 dimensions, this idea leads to Rochlin's theorem. It states that the signature of a 4-dimensional spin manifold is always divisible by 16. This is a surprising result that comes from the deep connections revealed by the index theorem.
Proof Techniques
Mathematicians have found different ways to prove the Atiyah–Singer index theorem.
Heat Equation
One popular way to prove the theorem uses the heat equation. Imagine heat spreading on a manifold. The heat equation describes how this happens. By looking at how the heat equation behaves for very short times, mathematicians can connect the analytical index to the topological index. This method involves some very clever cancellations that simplify complex calculations.
See also
 In Spanish: Teorema del índice de Atiyah-Singer para niños
In Spanish: Teorema del índice de Atiyah-Singer para niños