Compact space facts for kids

Per the compactness criteria for Euclidean space as stated in the Heine–Borel theorem, the interval A = (−∞, −2] is not compact because it is not bounded. The interval C = (2, 4) is not compact because it is not closed (but bounded). The interval B = [0, 1] is compact because it is both closed and bounded.

In mathematics, especially in a field called general topology, compactness is a special property for sets of points. It helps us understand what it means for a set to be "closed" and "bounded" in a more general way. Think of it like this: a compact space has no "holes" or "missing edges." It includes all the "limiting values" that points in the set can get close to.

For example, the open interval (0,1) is not compact. This is because it doesn't include the numbers 0 and 1, even though points inside the interval can get super close to them. But the closed interval [0,1] is compact because it includes both 0 and 1.

The set of rational numbers (fractions) is not compact. It has many "holes" where irrational numbers (like pi or the square root of 2) should be. The set of real numbers (all numbers on the number line) is also not compact because it goes on forever in both directions (to positive and negative infinity). However, if you add positive and negative infinity to the real number line, it does become compact!

There are different ways to define compactness. These definitions usually mean the same thing in a metric space (where you can measure distances). But they might be different in other types of topological spaces.

One way to think about it is "sequentially compact." This means that if you pick an endless number of points from the space, you can always find a smaller, endless group of those points that gets closer and closer to some point within that space.

The Bolzano–Weierstrass theorem tells us something important. For sets in Euclidean space (like a line, plane, or 3D space), a set is compact in this "sequential" way if it is both closed (has no missing boundary points) and bounded (doesn't go on forever).

So, if you pick an infinite number of points in the closed unit interval [0, 1], some of those points will get extremely close to a real number inside that interval. For instance, in the sequence 1/2, 4/5, 1/3, 5/6, 1/4, 6/7, ..., some numbers get closer and closer to 0, while others get closer to 1.

Since 0 and 1 are not part of the open interval (0, 1), those points wouldn't get close to any point inside that open interval. That's why the open interval is not compact. Also, a whole Euclidean space (like the entire number line) is not compact because it's not bounded. For example, the sequence 0, 1, 2, 3, ... on the real number line has no part that gets closer to any specific number.

The idea of compactness was first formally introduced by Maurice Fréchet in 1906. He wanted to extend the Bolzano–Weierstrass theorem from simple points to spaces of functions. Theorems like the Arzelà–Ascoli theorem show how this idea is used in math.

Later, other definitions of compactness were developed. The most common definition today, introduced by Pavel Alexandrov and Pavel Urysohn in 1929, uses "open covers." This idea helps us see compact spaces as a more general version of finite sets. In spaces that are compact in this way, it's often possible to take information that is true "locally" (around each point) and make it true "globally" (for the whole space). Many important math theorems work this way.

The term compact set can mean a compact space itself, or it can mean a compact part of a larger space.

A Little Bit of History

In the 1800s, mathematicians noticed several different properties that we now understand are related to compactness.

One idea came from Bernard Bolzano in 1817. He realized that any sequence of points that stays within a certain boundary (like on a line or a plane) must have a smaller sequence that gets closer and closer to some other point, called a limit point. Bolzano's proof used a method of "bisection." He would put the sequence into an interval, divide it in half, and pick the half that still contained an infinite number of points from the sequence. He repeated this process, making the intervals smaller and smaller, until they "closed in" on the limit point. The full importance of Bolzano's theorem wasn't fully understood until Karl Weierstrass rediscovered it almost 50 years later.

Around the 1880s, mathematicians like Giulio Ascoli and Cesare Arzelà started thinking about functions as "points" in a more general space. They found that similar ideas to Bolzano–Weierstrass could apply to spaces of functions. Their work led to the Arzelà–Ascoli theorem, which showed that you could find a "uniformly convergent" sequence of functions from a suitable group of functions. The limit of this sequence acted like Bolzano's "limit point."

At the start of the 20th century, David Hilbert and Erhard Schmidt also saw similar properties in their work on integral equations. This eventually led to the idea of a compact operator. It was Maurice Fréchet who, in 1906, brought all these ideas together and used the term compactness to describe this general mathematical behavior.

However, another idea of compactness also grew from studying the "continuum" (the idea of numbers being continuous, like on a line). In 1870, Eduard Heine showed that a continuous function on a closed and bounded interval was actually uniformly continuous. In his proof, he used a key idea: if you cover an interval with many smaller open intervals, you can always pick a finite number of those smaller intervals that still cover the original interval.

Émile Borel (1895) recognized how important this idea was. It was later generalized by Pierre Cousin (1895) and Henri Lebesgue (1904). This result is now known as the Heine–Borel theorem. It's another special property of closed and bounded sets of real numbers.

This property was important because it allowed mathematicians to take "local information" (like a function being continuous at every single point) and turn it into "global information" (like the function being uniformly continuous over the whole set). Pavel Alexandrov and Pavel Urysohn in 1929 developed this idea of Heine–Borel compactness so it could be used in modern topological spaces. They showed that Fréchet's earlier idea of compactness (now called sequential compactness) was related to this new idea of "finite subcovers." This "finite subcover" definition became the most common one because it was stronger and could be used in more general settings.

Simple Examples of Compact Spaces

Any space with a finite number of points is compact. You can always cover it with a finite number of open sets.

A good example of a compact space is the (closed) unit interval [0,1] of real numbers. If you pick an infinite number of different points in this interval, some of those points will always get very close to some point within that interval. For instance, the odd-numbered terms of the sequence 1, 1/2, 1/3, 3/4, 1/5, 5/6, 1/7, 7/8, ... get closer and closer to 0, while the even-numbered ones get closer and closer to 1.

This example shows why it's important to include the boundary points of the interval. The points that the sequence gets close to (the limit points) must be inside the space itself. An open interval (like (0,1)) or a half-open interval (like [0,1)) is not compact.

It's also important that the interval is bounded (doesn't go on forever). For example, in the interval [0,∞), you could pick the sequence of points 0, 1, 2, 3, .... No part of this sequence will ever get arbitrarily close to any specific real number.

In two dimensions, closed disks (like a solid coin) are compact. If you pick an infinite number of points from a disk, some of them will get very close to a point either inside the disk or on its edge. However, an open disk (like a coin without its edge) is not compact. This is because points can get closer and closer to the edge without ever reaching a point inside the open disk.

Similarly, spheres (like a solid ball) are compact. But a sphere with a missing point is not compact. Points can still get closer and closer to the missing point, but they won't get close to any point within the space that's left. Lines and planes are not compact because they are not bounded. You can pick equally spaced points that go on forever without getting close to any specific point.

What Does "Compact" Mean?

For a subset A of Euclidean space (like a line, plane, or 3D space), A is called compact if it is closed (contains all its boundary points) and bounded (doesn't go on forever). The Heine–Borel theorem confirms this. This means that any infinite sequence of points from the set will have a subsequence that gets closer and closer to a point within that set.

In general metric spaces (spaces where you can measure distances), different ideas of compactness, like sequential compactness (what we just talked about), are often the same.

However, in more general topological spaces, these ideas might not be the same. The most useful definition of compactness uses "covers" made of open sets. This is the standard definition.

When a space is compact in this way, it often lets us take information that is true "locally" (around each point) and make it true "globally" (for the entire space). For example, a continuous function on a compact interval is uniformly continuous. "Continuity" is a local property, and "uniform continuity" is the global property that comes from it.

Open Cover Definition

Formally, a topological space X is called compact if every way you can "cover" it with open sets has a finite "subcover."

Imagine you have a space X. An "open cover" is a collection of open sets that, when you put them all together, completely cover X. If X is compact, it means that no matter how many open sets you use to cover it, you can always find a finite number of those original open sets that still cover X.

Some mathematicians, especially those influenced by the French school of Bourbaki, use the term quasi-compact for this general idea. They save the term compact for spaces that are both "quasi-compact" and Hausdorff (which means distinct points have distinct neighborhoods).

Compactness of Subsets

A part K of a topological space X is called compact if it is compact when you consider it as its own smaller space. This means that if you cover K with open sets from the larger space X, you can always find a finite number of those open sets that still cover K.

Compactness is a "topological" property. This means if a set is compact within a smaller space, it's also compact within a larger space that contains it.

Key Characteristics of Compact Spaces

For a subset A of Euclidean space, A is compact if and only if it is closed and bounded. This is the Heine–Borel theorem. This is often the easiest way to check if a set is compact in Euclidean space, like checking if a closed interval or a closed ball is compact.

For any metric space (where you can measure distances), the following are equivalent:

• The space is compact.
• The space is complete (has no "missing" points) and totally bounded (can be covered by a finite number of small balls).
• The space is sequentially compact (every sequence has a convergent subsequence whose limit is in the space).
• Every infinite subset of the space has at least one limit point in the space.

A compact metric space also has these properties:

• It is second-countable, separable, and Lindelöf. These three conditions are the same for metric spaces.
• It is closed and bounded (as a subset of any metric space).

What Makes a Space Compact?

Here are some conditions that make a space compact:

• A closed part of a compact space is also compact.
• If you combine a finite number of compact sets, the result is also compact.
• If you have a continuous function and you apply it to a compact space, the resulting image is also compact.
• The intersection of any non-empty group of compact subsets in a Hausdorff space (where distinct points have distinct neighborhoods) is compact.
• The product of any group of compact spaces is compact. This is called Tychonoff's theorem.
• In a metrizable space (where you can define a distance), a subset is compact if and only if it is sequentially compact.
• Any finite set with any kind of topology is compact.

Properties of Compact Spaces

• A compact subset of a Hausdorff space is always closed.
• If two compact subsets in a Hausdorff space don't overlap, you can always find two separate open sets that contain them.
• A continuous one-to-one mapping from a compact space to a Hausdorff space is a homeomorphism (meaning it preserves the structure of the space).
• A compact Hausdorff space is normal and regular. These are special properties related to separating points and closed sets with open sets.
• If a space is compact and Hausdorff, you can't make its topology "finer" (add more open sets) and keep it compact. You also can't make its topology "coarser" (remove open sets) and keep it Hausdorff.
• If a part of a metric space is compact, then it is bounded.

Functions and Compact Spaces

Because a continuous image of a compact space is compact, an important rule called the extreme value theorem applies. This means that if you have a continuous function that gives you real numbers, and it's defined on a non-empty compact space, then the function will always have a maximum value and a minimum value.

Making Spaces Compact

Every topological space X can be made into a compact space by adding just one extra point. This is called the Alexandroff one-point compactification. For example, if you take the real number line and add one point for "infinity," it becomes like a circle S¹. If you take a plane and add one point for "infinity," it becomes like a sphere S².

Ordered Compact Spaces

A non-empty compact subset of the real numbers will always have a greatest element and a least element.

If a set is simply ordered (like numbers on a line) and has the order topology, then it is compact if and only if it is a complete lattice. This means all its subsets have a "least upper bound" and a "greatest lower bound."

More Examples of Compact Spaces

• Any finite topological space, including the empty set, is compact.
• Any space where only a finite number of sets are open is compact.
• Any space with the cofinite topology (where only sets with a finite number of points missing are open) is compact.
• The closed unit interval [0, 1] is compact. This is thanks to the Heine–Borel theorem. The open interval (0, 1) is not compact. You can cover it with open intervals like 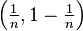(for n = 3, 4, ... ), but you can't pick a finite number of these to cover the whole open interval.
• The set 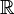of all real numbers is not compact. You can cover it with open intervals like (n − 1, n + 1)  (where n is any integer), but you can't pick a finite number of these to cover all real numbers.
• However, the extended real number line (which includes positive and negative infinity) is compact.
• For any natural number n, the n-sphere (like the surface of a ball in any dimension) is compact.
• The Cantor set is compact. In fact, every compact metric space can be seen as a continuous image of the Cantor set.
• Consider the set K of all functions f : 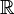→ [0, 1] (functions from the real line to the closed unit interval). If you define "convergence" as points getting closer for every input value, then K is a compact topological space. This comes from the Tychonoff theorem.
• The Hilbert cube is compact.

Images for kids

• 

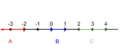
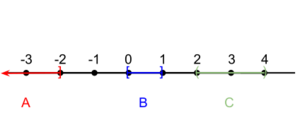
  Per the compactness criteria for Euclidean space as stated in the Heine–Borel theorem, the interval A = (−∞, −2] is not compact because it is not bounded. The interval C = (2, 4) is not compact because it is not closed (but bounded). The interval B = [0, 1] is compact because it is both closed and bounded.