Henri Lebesgue facts for kids

Quick facts for kids Henri Lebesgue
Born	(1875-06-28)June 28, 1875 Beauvais, Oise, France
Died	July 26, 1941(1941-07-26) (aged 66) Paris, France
Nationality	French
Alma mater	École Normale Supérieure University of Paris
Known for	Lebesgue integration< Lebesgue measure
Awards	Fellow of the Royal Society Poncelet Prize for 1914
Scientific career
Fields	Mathematics
Institutions	University of Rennes University of Poitiers University of Paris Collège de France
Doctoral advisor	Émile Borel
Doctoral students	Paul Montel Zygmunt Janiszewski Georges de Rham

Henri Léon Lebesgue (June 28, 1875 – July 26, 1941) was a French mathematician. He is famous for his theory of integration. This theory was a new way to calculate the area under a curve. It improved on older methods from the 1600s.

Lebesgue first shared his ideas in his university paper. It was called Intégrale, longueur, aire ("Integral, length, area"). He published it in 1902 at the University of Nancy.

Henri Lebesgue's Early Life and Education

Henri Lebesgue was born on June 28, 1875, in Beauvais, France. His father was a typesetter, and his mother was a school teacher. They had a library at home, which Henri used often.

Sadly, his father died young from tuberculosis. Henri's mother raised him alone. He showed great talent in mathematics from a young age. His teachers helped him get support to continue his studies. He went to schools in Beauvais and then in Paris.

In 1894, Lebesgue was accepted into the École Normale Supérieure. This is a top school for bright students. He focused on mathematics and graduated in 1897. He then worked in the school library for two years. There, he learned about new research on discontinuity.

He also started his advanced studies at the Sorbonne. He learned about measure theory from Émile Borel. In 1899, he began teaching at a high school in Nancy. At the same time, he kept working on his doctorate degree. In 1902, he earned his PhD from the Sorbonne. His important paper was on "Integral, Length, Area."

Family Life and Career Path

Henri Lebesgue married the sister of one of his classmates. They had two children, Suzanne and Jacques.

After finishing his PhD, Lebesgue got a job at the University of Rennes in 1902. He taught there until 1906. Then, he moved to the University of Poitiers. In 1910, Lebesgue moved to the Sorbonne in Paris. He became a professor there in 1919.

In 1921, he left the Sorbonne to teach at the Collège de France. He taught and did research there for the rest of his life. In 1922, he became a member of the Académie des Sciences. Henri Lebesgue passed away on July 26, 1941, in Paris.

Lebesgue's Contributions to Mathematics

Leçons sur l'integration et la recherche des fonctions primitives, 1904

Lebesgue's first math paper came out in 1898. It was about how to approximate functions. Between 1899 and 1901, he published several short notes. These notes led to his big work on Lebesgue integration.

His main work, Intégrale, longueur, aire, was published in 1902. In this work, he explained his new theory of "measure." This theory helps define the "size" of sets of numbers. He then used this idea to define his new type of integral. This paper is considered one of the best ever written by a mathematician.

Lebesgue also gave lectures that were turned into books. In these books, he explained the history of integration. He showed how his new method solved problems that older methods couldn't. He also worked on trigonometric functions and Fourier series. These are important in many areas of science and engineering.

He once wrote, "Reduced to general theories, mathematics would be a beautiful form without content." This means he believed math should be useful and have real-world meaning, not just abstract ideas.

Lebesgue's work had a huge impact on real analysis. This is a branch of mathematics that deals with real numbers and functions. His methods are now a key part of modern analysis.

Understanding Lebesgue's Integration Theory

Approximation of the Riemann integral by rectangular areas.

Integration is a math operation. It helps us find the area under the graph of a function. Imagine you want to find the area of a strange shape. Integration helps you do that.

The first ideas about integration came from Archimedes long ago. In the 1600s, Isaac Newton and Gottfried Wilhelm Leibniz found a link between integration and differentiation. Differentiation measures how fast a function changes. This link is called the Fundamental Theorem of Calculus. It allowed mathematicians to calculate many new integrals.

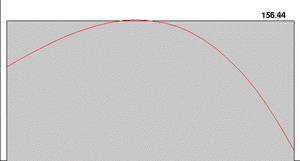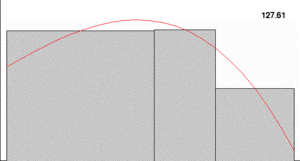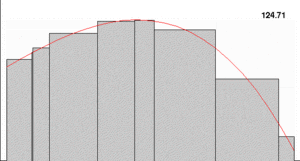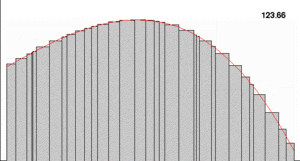
In the 1800s, Bernhard Riemann made the Riemann integral more formal. To do this, he filled the area under a graph with smaller and smaller rectangles. Then, he added up the areas of these rectangles. The total area would get closer to a single number. But for some functions, this method didn't work. The sum of the rectangle areas didn't settle on one number.

Lebesgue created a new way to integrate to fix this problem. Instead of focusing on the width of the rectangles (the "domain" of the function), Lebesgue focused on the height of the function (the "codomain").

Lebesgue's idea was to first define "measure." This is a way to assign a "size" to sets of numbers. Then, he built his integral for "simple functions." These are functions that take only a few specific values. After that, he defined the integral for more complex functions. He did this by finding the "least upper bound" of all the simple functions smaller than the function he was integrating.

The Lebesgue integral is very powerful. Any function that has a Riemann integral also has a Lebesgue integral. And for those functions, both integrals give the same answer. But many functions that don't have a Riemann integral can be integrated using Lebesgue's method.

As part of his work, Lebesgue invented the idea of measure. This extends the idea of length from simple intervals to a much wider range of sets.

While the Riemann integral can be extended to "improper" integrals for functions over infinite ranges, the Lebesgue integral handles many of these cases directly. However, there are some functions that the Lebesgue integral doesn't cover. Other types of integrals, like the Henstock integral, can handle even more cases. But the Lebesgue integral is very important because it can be used in many different mathematical spaces, not just on the real number line.

See also