Fundamental theorem of calculus facts for kids

The fundamental theorem of calculus is a super important idea in calculus. It helps us understand the special connection between two big parts of calculus: the derivative and the integral. It also links definite integrals and indefinite integrals. This theorem has two main parts.

Understanding Calculus Basics

To understand this theorem, it helps to know what a derivative, a definite integral, and an indefinite integral are.

• A derivative tells us how fast something is changing. Imagine you are driving a car. Your speed is the derivative of your distance over time. It shows how your distance changes with each moment.
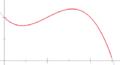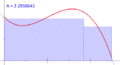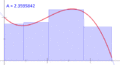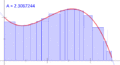
• A definite integral helps us find the total area under a curve. Think of a graph of a function. The definite integral calculates the exact area between the function's line and the x-axis over a specific range.
• An indefinite integral (also called an antiderivative) is like doing the opposite of a derivative. If you have a function, its antiderivative is another function. When you take the derivative of this new function, you get back to your original one.

A Brief History of the Theorem

The ideas behind the fundamental theorem of calculus started way back in the 1600s. Two brilliant mathematicians, Gottfried Wilhelm Leibniz and Isaac Newton, played a huge role.

• Leibniz thought of integration as adding up tiny, tiny areas. He saw how finding the area was connected to the idea of an integral.
• Newton used geometry to explain how things like distance, speed (velocity), and how fast speed changes (acceleration) are related. He showed that acceleration is the derivative of velocity, and velocity is the derivative of distance. This also means distance is the antiderivative of velocity, and velocity is the antiderivative of acceleration. This was a key step in seeing the link between derivatives and integrals.

Later, in the 1800s, other mathematicians added to these ideas.

• In 1823, Cauchy gave a clear definition for the definite integral.
• Siméon Denis Poisson described how the definite integral could be found by subtracting antiderivatives at two points. This is very close to what we now call the first fundamental theorem.

It wasn't until the 1950s that all these ideas were officially brought together and named the "fundamental theorem of calculus."

Second Fundamental Theorem of Calculus

The second fundamental theorem of calculus shows that derivatives and integrals are opposite operations. They undo each other! It says that if you have a continuous function called f, then:

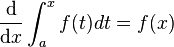
In simpler words, if you take the derivative of an integral of a function, you get the original function back. It's like adding 5 and then subtracting 5 – you end up where you started!

First Fundamental Theorem of Calculus

The first fundamental theorem of calculus gives us a powerful way to calculate definite integrals. It states that if a function f(x) is continuous, then:

This animation shows how the area under a curve (the integral) can be found using the antiderivative.

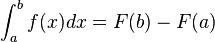
This means that to find the definite integral of a function over an interval from 'a' to 'b', you just need to find its antiderivative (F). Then, you calculate the value of the antiderivative at 'b' and subtract its value at 'a'. This makes finding areas under curves much easier!

Images for kids

• 

  Fundamental theorem of calculus (animation)

• 

  A converging sequence of Riemann sums. The number in the upper left is the total area of the blue rectangles. They converge to the definite integral of the function.

See also

In Spanish: Teorema fundamental del cálculo para niños