Binary search algorithm facts for kids
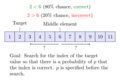
Visualization of the binary search algorithm where 7 is the target value
|
|
| Class | Search algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | O(log n) |
| Best-case performance | O(1) |
| Average performance | O(log n) |
| Worst-case space complexity | O(1) |
Imagine you have a super long list of names, all sorted alphabetically. If you want to find one specific name, how would you do it? You could start from the beginning and check each name one by one. That's called a linear search. But what if the list has a million names? That would take forever!
This is where binary search comes in handy. It's a clever way to find something in a sorted list much faster. Think of it like playing "20 Questions" with numbers. You guess the middle, and then you know if your number is higher or lower. This helps you cut the search area in half every time!
Binary search is super fast for big lists. It's used a lot in computer science to find things quickly in sorted arrays. An array is like a list where items are stored in order. Even though other methods exist, binary search is great for finding items, or even finding items that are close to what you're looking for.
Contents
How Does Binary Search Work?
Binary search only works if your list (or array) is already sorted. If it's not, you need to sort it first!
Here's the basic idea:
- You start by looking at the item exactly in the middle of your sorted list.
- If that middle item is what you're looking for, great! You found it.
- If the item you're looking for is smaller than the middle item, you know it must be in the first half of the list.
- If the item you're looking for is larger than the middle item, you know it must be in the second half of the list.
- Then, you repeat the process! You take the half of the list where your item could be, find its new middle, and check again.
- You keep doing this, cutting the list in half each time, until you find your item or there's nothing left to search.
This way, you quickly get rid of half of the remaining items in every step.
Step-by-Step Example
Let's say you have a list of numbers: `[10, 20, 30, 40, 50, 60, 70, 80, 90]` and you want to find the number `70`.
- Step 1: The whole list is `[10, 20, 30, 40, 50, 60, 70, 80, 90]`.
* The middle element is `50`. * Is `70` equal to `50`? No. * Is `70` smaller than `50`? No. * Is `70` larger than `50`? Yes. * So, we only need to search the right half: `[60, 70, 80, 90]`.
- Step 2: Our new list is `[60, 70, 80, 90]`.
* The middle element is `70` (or `80` depending on how you pick the middle). Let's say it's `70`. * Is `70` equal to `70`? Yes! * You found it! The search is over.
This process is much faster than checking each number one by one.
What if There are Duplicates?
Sometimes, your list might have the same number more than once. For example: `[1, 2, 4, 4, 4, 5, 6, 7]`. If you search for `4`, binary search might find any of the `4`s.
There are special ways to change the binary search steps if you specifically need to find:
- The first `4` in the list.
- The last `4` in the list.
These changes involve slightly different rules for moving your search boundaries.
Finding Close Matches
Binary search isn't just for finding exact matches. Because it works on sorted lists, it can also help you find:
- The number of items smaller than your target.
- The item just before your target (the "predecessor").
- The item just after your target (the "successor").
- The item closest to your target.
This makes binary search very useful for many different kinds of problems.
How Fast is Binary Search?
Binary search is incredibly fast, especially for large lists.
Think about how many steps it takes. Each time, you cut the list in half.
- If you have 100 items, after 1 step, you have 50.
- After 2 steps, you have 25.
- After 3 steps, you have about 12.
- And so on.
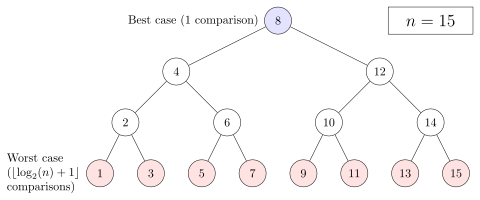
This means that even for a list with a million items, binary search will find your item in about 20 steps! This is because it takes roughly the logarithm (base 2) of the number of items. In computer science, we say this is O(log n).
- Best Case: If the item you're looking for happens to be the very first middle element you check, it takes only one step!
- Worst Case: The most steps it will ever take is when you have to keep dividing until only one item is left. This is still very fast compared to checking every item.
Binary search is one of the fastest ways to search a sorted list using comparisons. No other method that just compares items can be faster on average or in the worst case.
Memory Use
Binary search doesn't need much extra memory. It only needs a few variables to keep track of where it's searching in the list. So, it uses very little computer memory, no matter how big the list is.
Binary Search Compared to Other Methods
Binary search is powerful, but it's not always the best choice for every situation.
Linear Search vs. Binary Search
- Linear Search: Checks every item one by one. It's simple and works on any list, even unsorted ones. But it's very slow for large lists.
- Binary Search: Much faster for large, sorted lists. But the list must be sorted first.
If your list is small, linear search might actually be quicker because binary search has a few more setup steps. But for anything big, binary search wins!
Trees vs. Binary Search
A binary search tree is a special way to organize data that works a lot like binary search. It's like a family tree, but for numbers! Each "node" (like a person in the family tree) has a value. Smaller values go to the left, and larger values go to the right.
- Searching in a binary search tree is similar to binary search and is also very fast.
- The cool thing about trees is that you can also add or remove items quickly, which is harder to do with a simple sorted list.
- However, binary search on a simple sorted list can sometimes be a tiny bit faster for just searching, because trees can sometimes get a little "unbalanced."
Hashing vs. Binary Search
Hash tables are another way to store and find information. They use a special "hash function" to figure out exactly where an item should be stored.
- Hashing: Can find items super fast, often in just one step!
- Binary Search: Great for finding exact matches, but also for finding items that are "close" to what you're looking for (like the next smallest or largest). Hashing can't do this easily.
So, if you only need to find exact items and don't care about "close" ones, hashing might be faster. But if you need to find things in order or find approximate matches, binary search is better.
Different Kinds of Binary Search
There are many cool variations of binary search that help with specific problems:
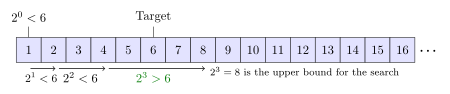
Exponential Search
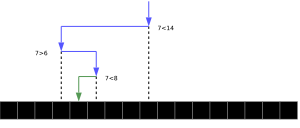
Imagine you have an incredibly long list, but you don't even know how long it is! Exponential search helps here. It first quickly finds a small section where your item might be, and then uses regular binary search on that section. It's like finding the right chapter in a book before looking for a specific word.
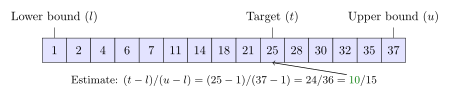
Interpolation Search
Regular binary search always picks the middle. But what if you're looking for the number `99` in a list from `1` to `100`? The middle is `50`. Interpolation search is smarter. It tries to guess where the item might be based on its value. If `99` is close to `100`, it will guess a spot closer to the end of the list. This can be even faster than binary search for certain types of data.
Fractional Cascading
What if you need to search for the same item in many different sorted lists? Doing a separate binary search for each list would take a lot of time. Fractional cascading is a clever trick that links these lists together. It lets you search all of them much faster, by only doing one main search and then quickly jumping between the linked lists.
History of Binary Search
People have been sorting lists to make them easier to search for a very long time!
- One of the earliest examples is an ancient tablet from Babylon, around 200 BCE, which had numbers and their opposites sorted in order.
- In 1286 CE, a Latin dictionary called Catholicon was the first to describe rules for sorting words alphabetically.
The idea of binary search as we know it in computers was first mentioned by John Mauchly in 1946. For a while, binary search only worked perfectly on lists that had a very specific number of items (like 7, 15, 31, etc.). But in 1960, Derrick Henry Lehmer created a version that worked for lists of any size.
Even though the idea seems simple, writing the computer code for binary search can be tricky! Famous computer scientist Donald Knuth once said that "the details can be surprisingly tricky." Many programmers have made small mistakes in their code that cause it to fail in rare situations. This shows how important it is to be very careful when writing computer programs.
Using Binary Search in Programming
Because binary search is so useful, many programming languages have it built right into their standard libraries. This means you don't have to write the code yourself! You can just use a ready-made function.
For example:
- C++ has functions like `binary_search()`.
- Java has `binarySearch()` methods.
- Python has a `bisect` module.
- Ruby includes a `bsearch` method.
These built-in tools make it easy for programmers to use the power of binary search without worrying about all the tricky details.
Images for kids
-
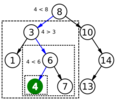
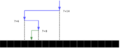
A tree representing binary search. The array being searched here is
![[20, 30, 40, 50, 80, 90, 100]](/images/math/c/1/8/c18502620b351be9034e391a2bc1a129.png) , and the target value is
, and the target value is 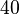 .
.
See also
 In Spanish: Búsqueda binaria para niños
In Spanish: Búsqueda binaria para niños
 | Aaron Henry |
 | T. R. M. Howard |
 | Jesse Jackson |




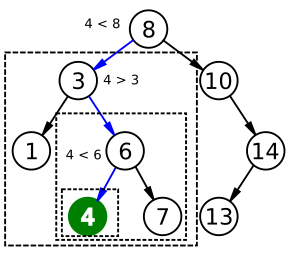
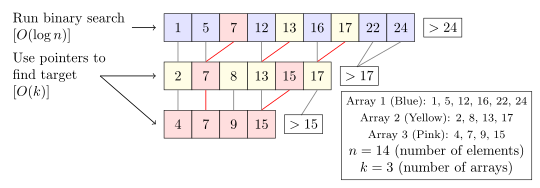


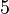 , which is not in the array.
, which is not in the array.