Combinatorial optimization facts for kids

Combinatorial optimization is a fascinating part of mathematics that helps us find the very best way to do things. Imagine you have many choices, and you want to pick the one that is the most efficient, cheapest, or fastest. That's what this field is all about! It helps solve problems where you need to choose items from a group or arrange them in the perfect order.

What is Combinatorial Optimization?

Combinatorial optimization is a special area of discrete mathematics. "Discrete" means we are dealing with things that can be counted, like whole numbers, rather than smooth, continuous things. This field focuses on finding the "optimal" (best) object or arrangement from a set of many possible choices.

Think of it like this:

• You have a puzzle with many pieces. Combinatorial optimization helps find the best way to put them together.
• You have a list of tasks. It helps find the best order to do them to finish fastest.

The goal is always to find the solution that is "best" according to some rules. This could mean finding the shortest path, the lowest cost, or the most efficient schedule.

Real-World Puzzles Solved by Optimization

Many real-world problems can be turned into combinatorial optimization puzzles. These problems often have a huge number of possible solutions. Finding the best one by just trying every option would take too long, even for powerful computers!

The Traveling Salesman Problem

One famous example is the Traveling Salesman Problem (TSP). Imagine a delivery person who needs to visit several cities and then return home. The challenge is to find the shortest possible route that visits each city exactly once.

• This problem sounds simple, but it gets very hard very quickly.
• If you have only a few cities, you can list all possible routes.
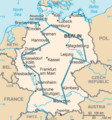
• With many cities, the number of routes becomes enormous. For example, with just 15 cities, there are over 43 billion possible routes!
• Combinatorial optimization uses smart methods to find the shortest route without checking every single one.

Minimum Spanning Tree

Another important problem is finding the Minimum spanning tree in a graph. A graph is like a network of dots (called "nodes" or "vertices") connected by lines (called "edges"). Imagine these dots are towns and the lines are roads.

• A "spanning tree" connects all the towns without any loops.
• A "minimum spanning tree" is the one where the total length of all the roads is as short as possible.
• This is useful for designing efficient networks, like laying out power lines or internet cables.

How Problems Are Solved

Solving combinatorial optimization problems often involves clever computer algorithms. These are like step-by-step recipes that computers follow.

• Some problems can be solved using linear programming. This is a mathematical method for finding the best outcome (like maximum profit or lowest cost) in a mathematical model.
• Other problems might use special search techniques that explore possible solutions in a smart way, avoiding paths that clearly won't lead to the best answer.
• Sometimes, even if we can't find the absolute best solution quickly, we can find a "good enough" solution that is very close to the best.

Why is it Important?

Combinatorial optimization is used in many different areas:

• Logistics and Delivery: Planning efficient delivery routes for packages or food.
• Manufacturing: Scheduling production lines to make the most products with the least waste.
• Telecommunications: Designing efficient networks for phones and the internet.
• Finance: Choosing the best investments or managing portfolios.
• Science: Designing experiments or analyzing data.

It helps businesses save money, makes services more efficient, and solves complex challenges in our modern world.

Images for kids

• 

  An optimal traveling salesperson tour through Germany’s 15 largest cities. It is the shortest among the 43,589,145,600 possible tours that visit each city exactly once.

See also

In Spanish: Optimización combinatoria para niños