Commutative diagram facts for kids

This is a commutative diagram used in a math proof called the five lemma.

In mathematics, especially in a field called category theory, a commutative diagram is a special kind of drawing. Imagine a map where you can go from one place to another using different paths. If all paths starting and ending at the same points always lead to the same result, then that's what a commutative diagram shows! These diagrams are very important in category theory, just like equations are important in algebra. They help us understand how different mathematical ideas are connected.

What is a Commutative Diagram?

A commutative diagram is made up of a few key parts:

• Objects: These are like the 'places' or 'points' in our diagram. They are often shown as circles or boxes.
• Morphisms: These are like the 'paths' or 'arrows' that connect the objects. They show how one object relates to another.
• Paths or Composites: These are the different ways you can travel from one object to another by following the arrows.

Understanding the Arrows

Sometimes, the arrows in these diagrams have special meanings, especially in advanced algebra:

• An arrow like or can mean an 'injection'. Think of it as putting one group of things *into* another group without losing any of the original things.
• An arrow like 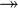can mean a 'surjection'. This is like making sure every item in the second group is 'hit' by something from the first group.
• An arrow like can mean an 'isomorphism'. This means two objects are basically the same, just seen in a different way.
• A dashed arrow usually means that a connection or 'morphism' *should* exist. If it has a '!' sign, it means that connection is also unique (there's only one way to make it).

It's good to know that these arrow meanings can sometimes change depending on the specific math topic!

Checking if a Diagram Commutes

A diagram 'commutes' if all the different paths between any two objects give you the same final result. You can check this by looking at smaller shapes within the diagram, like triangles or squares. If all these smaller shapes commute, then the whole diagram commutes!

Sometimes, a diagram might be 'non-commutative'. This means that taking different paths between the same two points might lead to different results.

Examples of Commutative Diagrams

Let's look at some simple examples to see how they work.

Example 1: Triangles and Squares

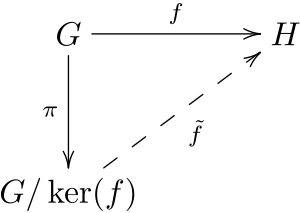
In the diagram on the left, we have a triangle. For this triangle to commute, it means that going directly from one point to another (like 'f') is the same as taking a two-step path (like 'pi' then 'f-tilde').

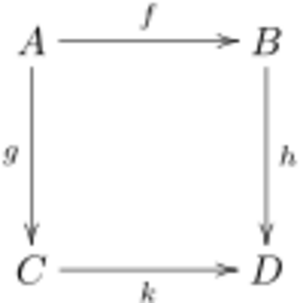
The diagram on the right shows a square. For this square to commute, it means that if you go from the top-left to the bottom-right by going right then down (h then f), it's the same as going down then right (k then g). So, `h` followed by `f` must be the same as `k` followed by `g`.

This triangle diagram shows how different paths can be equal.

This square diagram shows that two different paths lead to the same result.

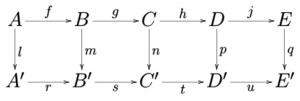
Example 2: A More Complex Diagram

For the diagram below to commute, three specific relationships must be true:

1. Going `l` then `G` then `H` must be the same as going `g` then `h` then `r`.
2. Going `l` then `G` must be the same as going `g` then `m`.
3. Going `h` then `r` must be the same as going `m` then `H`.

If the second and third relationships are true, then the first one will automatically be true! This means you only need to check the simpler parts to make sure the whole diagram commutes.

A more complex commutative diagram with multiple paths.

Diagram Chasing

Diagram chasing is a clever way to prove things in mathematics, especially in a field called homological algebra. It's like being a detective and following clues around a commutative diagram.

When you do a diagram chase, you use the properties of the arrows (like if they are 'injective' or 'surjective') and the fact that the diagram commutes. You trace elements (mathematical 'things') along the arrows, step by step, until you can prove what you want to show. The diagram itself is a visual guide, helping you keep track of your steps.

Famous proofs that use diagram chasing include the five lemma, the snake lemma, and the zig-zag lemma.

Images for kids

• 

  This diagram shows categories, functors (arrows), and natural transformations (double arrows) in higher category theory.