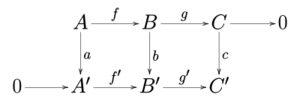Homological algebra facts for kids
Homological algebra is a part of mathematics that looks at "holes" or "connections" in mathematical objects using tools from algebra. It's like using a special magnifying glass to find hidden patterns and structures.
This field started to grow in the late 1800s, thanks to mathematicians like Henri Poincaré and David Hilbert. They were studying shapes and abstract number systems.
A main idea in homological algebra is called a chain complex. Think of it as a sequence of mathematical "boxes" connected by "arrows." Homological algebra helps us understand these boxes and arrows, and what they tell us about the original objects.
This area of math is very useful. It helps mathematicians understand many different things, from the shapes of spaces to the properties of numbers and equations. It's used in areas like algebraic topology (studying shapes), algebraic geometry (studying shapes using algebra), and even mathematical physics.
Contents
History of Homological Algebra
Homological algebra first appeared in the 1800s as a part of topology, which is the study of shapes. However, it only became its own separate subject in the 1940s. At that time, mathematicians started to deeply study special mathematical tools called the ext functor and the tor functor.
Understanding Chain Complexes and Homology
The idea of a chain complex is super important in homological algebra. Imagine a line of boxes, each holding a group of numbers or objects. These boxes are connected by special arrows (called "maps" or "differentials").
Here's how it works:
- You have a sequence of groups, like C~n+1~, C~n~, C~n-1~.
- Arrows (d~n+1~, d~n~, d~n-1~) connect them.
- A key rule is that if you follow two arrows in a row, you always end up with zero. This means `d~n~` followed by `d~n+1~` equals zero.
The objects inside the boxes (C~n~) are called n-chains. The arrows (d~n~) are called boundary maps or differentials. These groups can be simple numbers or more complex mathematical structures like vector spaces.
From a chain complex, we can find two other important groups:
- Cycles (Z~n~): These are the elements in a box that become zero when you apply the next arrow.
- Boundaries (B~n~): These are the elements that come from applying an arrow from the previous box.
Because of the "two arrows make zero" rule, all boundaries are also cycles. This means the boundaries are "inside" the cycles.
The n-th homology group (H~n~(C)) is found by taking the cycles and "dividing out" the boundaries. It tells us what's left over after we remove the parts that are boundaries. If all homology groups are zero, the chain complex is called acyclic or an exact sequence.
Chain complexes show up in many areas of math. For example:
- In algebraic topology, they help us understand the properties of topological spaces (like surfaces or knots).
- They can also describe how groups of numbers are built from smaller parts.
Homological algebra helps us get valuable information from these chain complexes. The homology groups are just one part of this information.
- If you have two objects (like two shapes) connected by a map, homological algebra helps us see how their chain complexes and homology groups are related.
- Sometimes, an object can be described in different ways. Homological algebra shows that even if the chain complex looks different, the homology groups will be the same. This means homology groups are a true "fingerprint" or invariant of the object.
Important Tools in Homological Algebra
Exact Sequences
An exact sequence is a chain of mathematical groups and maps where the "output" of one map is exactly the "input" of the next map.
Imagine a factory line: `G~0~` → `G~1~` → `G~2~` → `G~3~` For this to be exact, everything produced by the first machine (`f~1~`) must be exactly what the second machine (`f~2~`) needs to start its work.
This idea works for different types of mathematical groups, like vector spaces or modules.
Short Exact Sequence
The most common type is a short exact sequence. It looks like this: `A` → `B` → `C` Here, `A` fits perfectly inside `B`, and `C` is what you get when you "divide" `B` by `A`.
Often, it's written with zeros at the ends: `0` → `A` → `B` → `C` → `0` The zeros make sure that the first map puts `A` perfectly into `B`, and the last map covers all of `C`.
Long Exact Sequence
A long exact sequence is simply an exact sequence that goes on for many steps, often indexed by numbers.
The Five Lemma
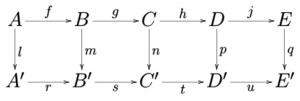
The five lemma is a powerful tool used in abelian categories (like the category of abelian groups). Imagine two parallel exact sequences, connected by vertical maps, forming a grid.
If the top and bottom rows are exact, and four of the five vertical maps are isomorphisms (meaning they are perfect matches), then the middle vertical map must also be an isomorphism. It's like if four out of five bridges are perfect, the fifth one must be perfect too!
The Snake Lemma
The snake lemma is another important tool in abelian categories. It's used when you have a specific kind of grid diagram with two exact rows.
If you have a diagram like the one shown, where the rows are exact, the snake lemma tells you that there's a special exact sequence connecting the "kernels" (what maps to zero) and "cokernels" (what's left over after mapping) of the vertical maps. It's called the "snake" lemma because the sequence it creates looks like a snake winding through the diagram!
Abelian Categories
An abelian category is a special kind of mathematical category where you can add objects and maps, and where certain operations (like finding kernels and cokernels) always work nicely. The most basic example is the category of abelian groups (groups where the order of addition doesn't matter, like regular numbers).
Abelian categories are very "stable" and well-behaved. They are important because many results in homological algebra, like the snake lemma, work in any abelian category.
The Ext Functor
The Ext functor is a tool in homological algebra that helps us understand how two mathematical modules are related. It measures "how far" a certain operation (called Hom) is from being "exact."
Imagine you have two modules, A and B. The Ext functor, written as `Ext^n^~R~(A,B)`, gives you a series of groups that tell you about the ways A can be "extended" by B. It's calculated using special sequences called "resolutions."
Tor Functor
The Tor functor is another tool, similar to the Ext functor. It's also used to understand relationships between modules, but it uses a different operation called the tensor product.
The Tor functor, written as `Tor^n^~R~(A,B)`, also measures "how far" the tensor product is from being "exact." It's calculated using "projective resolutions" of modules.
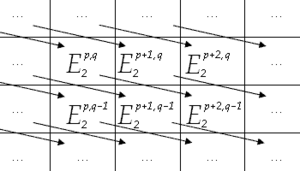
Spectral Sequence
A spectral sequence is a powerful way to organize a lot of complex mathematical information. Think of it as a stack of graph paper sheets. On each sheet, you have a grid of mathematical objects.
As you move from one sheet to the next (from `E~r~` to `E~r+1~`), the information changes in a structured way. There are "boundary maps" that move objects around on each sheet, and the next sheet is formed from the "homology" of the previous one.
Spectral sequences help mathematicians solve very difficult problems by breaking them down into smaller, more manageable steps. The way the "differentials" (arrows) move objects on the grid can be compared to chess moves, like a knight's move!
Derived Functor
A derived functor is a general idea in homological algebra. If you have a mathematical operation (a "functor") that doesn't quite preserve "exactness" (meaning it might break an exact sequence), derived functors measure exactly how much it breaks it.
They help us extend short exact sequences into longer ones, revealing more information about the mathematical objects involved.
How Homological Algebra Connects Things
Homological algebra is great at showing how different mathematical objects are related. For example, if you have a continuous map between two topological spaces (like stretching a rubber band from one shape to another), this map creates a connection between their homology groups.
A morphism between two chain complexes is like a map that connects them, making sure the arrows line up correctly. This map then creates a map between their homology groups. If a morphism makes all homology groups match perfectly, it's called a quasi-isomorphism.
Many ways of building chain complexes have a special property called functoriality. This means if you have maps between objects, you also get maps between their chain complexes and their homology groups. This helps us understand how changes in one object affect its related mathematical structures.
A short exact sequence of complexes is when you have three chain complexes lined up, and each "slice" of them forms a short exact sequence. A very important theorem in homological algebra, called the zig-zag lemma, says that if you have such a sequence, you can always build a long exact sequence in homology. This long sequence connects the homology groups of all three complexes in a continuous chain. This theorem is used in topology to create sequences like the Mayer–Vietoris sequence.
Why Homological Algebra is Important
Homological algebra provides a common way to understand many different "cohomology theories" that exist for various mathematical objects, like topological spaces, groups, and rings. It's a key part of modern algebraic geometry.
The idea of the exact sequence is central, as it allows for actual calculations. Tools like derived functors (Ext and Tor) are fundamental.
Mathematicians have worked to put all these ideas on a strong, unified foundation. Some key developments include:
- The work of Henri Cartan and Samuel Eilenberg in 1956, using special "resolutions" of modules.
- Alexander Grothendieck's work in 1957, which used the concept of abelian categories to make the theory more general.
- The development of "derived categories" by Grothendieck and Jean-Louis Verdier in the 1960s, which are even more abstract but very powerful.
These developments moved the field from being focused on specific calculations to being very general. Even with these general theories, spectral sequences remain a vital tool for doing actual calculations.
See also
 In Spanish: Álgebra homológica para niños
In Spanish: Álgebra homológica para niños
- Abstract nonsense, a playful term sometimes used for homological algebra and category theory
- Homotopical algebra
- List of homological algebra topics