Henri Poincaré facts for kids

Quick facts for kids Henri Poincaré
Henri Poincaré (photograph published in 1913)
Born	(1854-04-29)29 April 1854 Nancy, Meurthe-et-Moselle, France
Died	17 July 1912(1912-07-17) (aged 58) Paris, France
Nationality	French
Other names	Jules Henri Poincaré
Education	Lycée Nancy (now Lycée Henri-Poincaré [fr]) École Polytechnique École des Mines University of Paris (Dr, 1879)
Known for	Poincaré conjecture Poincaré–Bendixson theorem Poincaré–Lindstedt method Poincaré recurrence theorem Poincaré–Bjerknes circulation theorem Poincaré group Poincaré gauge Poincaré–Hopf theorem Poincaré duality Poincaré–Birkhoff–Witt theorem Poincaré inequality Hilbert–Poincaré series Poincaré series Poincaré metric Automorphic form Coining the term "Betti number" Brouwer fixed-point theorem Bifurcation theory Chaos theory Dynamical system theory French historical epistemology Fundamental group Gravitational wave Hairy ball theorem Homological algebra Limit cycle Phase space Preintuitionism/conventionalism Predicativism Qualitative theory of differential equations Special relativity Sphere-world Rotation number Uniformization theorem Three-body problem Topology
Awards	RAS Gold Medal (1900) Sylvester Medal (1901) Matteucci Medal (1905) Bolyai Prize (1905) Bruce Medal (1911)
Scientific career
Fields	Mathematics and physics
Institutions	Corps des Mines Caen University La Sorbonne Bureau des Longitudes
Thesis	Sur les propriétés des fonctions définies par les équations différences (1879)
Doctoral advisor	Charles Hermite
Doctoral students	Louis Bachelier Jean Bosler Dimitrie Pompeiu Mihailo Petrović
Other notable students	Tobias Dantzig Théophile de Donder
Influences	Lazarus Fuchs Immanuel Kant Ernst Mach
Influenced	Louis Rougier George David Birkhoff Albert Einstein
Signature
Notes
He was an uncle of Pierre Boutroux.

Jules Henri Poincaré (UK: /ˈpwæ̃kɑːreɪ/ [US: stress final syllable], French: [ɑ̃ʁi pwɛ̃kaʁe] ; 29 April 1854 – 17 July 1912) was a brilliant French mathematician, physicist, engineer, and philosopher. People often called him a polymath because he was an expert in many different fields. In mathematics, he was known as "The Last Universalist" because he was skilled in all areas of math during his time.

As a mathematician and physicist, he made many important discoveries. These discoveries helped shape pure and applied mathematics, mathematical physics, and celestial mechanics (the study of how planets and stars move). For example, he was the first to find a chaotic deterministic system while studying the three-body problem. This work helped create modern chaos theory. He is also seen as one of the people who started the field of topology, which is about the shapes of objects.

Poincaré also showed how important it was for the laws of physics to stay the same even when things change. He was the first to write down the Lorentz transformations in their modern, balanced form. These transformations are key to understanding how space and time are connected. In 1905, he also suggested that gravitational waves exist. These waves would travel at the speed of light, as required by the Lorentz transformations.

The Poincaré group, a concept used in physics and mathematics, is named after him. He also came up with the Poincaré conjecture in the early 1900s. This was a famous unsolved math problem for many years until Grigori Perelman solved it in 2002–2003.

Henri Poincaré's Life Story

Henri Poincaré was born on April 29, 1854, in Nancy, France. He came from an important French family. His father, Léon Poincaré, was a medicine professor. His cousin, Raymond Poincaré, later became the President of France.

His Education and Early Years

A plaque on Henri Poincaré's birthplace in Nancy, France.

When Henri was a child, he got very sick with diphtheria. His mother taught him at home for a while. In 1862, he started at the Lycée in Nancy. This school is now named the Lycée Henri-Poincaré [fr] in his honor.

Henri spent eleven years at the Lycée and was a top student in every subject. His math teacher called him a "monster of mathematics." He won many top awards in national competitions. However, he wasn't very good at music or physical education. This might have been because he had poor eyesight and was often lost in thought. He finished school in 1871.

During the Franco-Prussian War in 1870, he helped his father in the Ambulance Corps.

In 1873, Poincaré entered the École Polytechnique, a famous engineering school, as the top student. He continued to do well in math and published his first paper in 1874. He also studied at the École des Mines and became a mining engineer in 1879.

After graduating, he worked as a mining inspector. He even helped investigate a mining accident where 18 miners died. He did this work very carefully and with care for others.

At the same time, he was working on his doctorate in mathematics. His thesis was about differential equations. He found a new way to study these equations and how they could be used to understand how multiple bodies move in space. He earned his doctorate from the University of Paris in 1879.

A photo of Henri Poincaré in 1887, when he was 33 years old.

First Big Discoveries

After getting his degree, Poincaré started teaching math at the University of Caen in 1879. There, he published his first important paper on a type of math called automorphic functions.

In Caen, he met Louise Poulain d'Andecy, and they married in 1881. They had four children together.

Poincaré quickly became known as one of Europe's greatest mathematicians. In 1881, he was invited to teach at the University of Paris. From 1883 to 1897, he taught mathematical analysis at the École Polytechnique.

In 1881–1882, Poincaré created a new area of math called the qualitative theory of differential equations. He showed how to learn important things about solutions to equations without actually solving them. He used this method to solve problems in celestial mechanics and mathematical physics.

His Career and Achievements

Poincaré never fully stopped working in mining. He worked for the Ministry of Public Services from 1881 to 1885. He later became a chief engineer in 1893 and an inspector general in 1910.

From 1881 onwards, he taught at the University of Paris (the Sorbonne). He held different positions, including professor of Physical and Experimental Mechanics, Mathematical Physics, and Celestial Mechanics.

In 1887, at just 32 years old, Poincaré was chosen to join the French Academy of Sciences. He became its president in 1906. He was also elected to the Académie française in 1908.

In 1887, he won a math competition set up by King Oscar II of Sweden. The competition was about the three-body problem, which asks how three orbiting objects move. Poincaré didn't fully solve the original problem, but his work was so important that he still won the prize. His ideas led to the theory of chaos.

In 1893, Poincaré joined the French Bureau des Longitudes. This group worked on synchronizing time around the world. This work made him think about how to set up international time zones. It also made him consider how clocks would work when they were moving relative to each other.

In 1904, he helped in the trials of Alfred Dreyfus. Poincaré showed that some scientific claims used against Dreyfus were false.

Poincaré was also the president of the French astronomical society from 1901 to 1903.

His Students

Poincaré had two important students who earned their doctorates under him: Louis Bachelier (1900) and Dimitrie Pompeiu (1905).

His Death

In 1912, Poincaré had surgery for a health issue. Sadly, he died from a blood clot on July 17, 1912, in Paris. He was 58 years old. He is buried in the Poincaré family tomb in the Cemetery of Montparnasse in Paris.

The Poincaré family grave at the Cimetière du Montparnasse.

In 2004, a former French Minister of Education suggested that Poincaré should be reburied in the Panthéon in Paris. This is a special place for France's most honored citizens.

Henri Poincaré's Work and Discoveries

Summary of His Contributions

Poincaré made many contributions to different areas of math and physics. These included celestial mechanics (how things move in space), fluid mechanics (how liquids and gases move), optics (light), electricity, telegraphy, capillarity (how liquids move in narrow spaces), elasticity (how things stretch), thermodynamics (heat and energy), potential theory, quantum theory, theory of relativity, and physical cosmology (the study of the universe).

He also wrote several books to help everyday people understand math and physics.

Here are some of the specific topics he worked on:

• algebraic topology (a field he practically invented)
• hyperbolic geometry
• number theory
• the three-body problem
• electromagnetism
• the special theory of relativity
• the fundamental group
• Poincaré recurrence theorem (about systems returning to a similar state)
• Poincaré conjecture (a famous math problem he proposed)

The Three-Body Problem

For a long time, mathematicians couldn't figure out how to perfectly predict the motion of more than two orbiting bodies in space. This was called the three-body problem. In 1887, King Oscar II of Sweden offered a prize to anyone who could solve it.

Poincaré won the prize, even though he didn't completely solve the original problem. His work was so important that one judge said it would "start a new era in the history of celestial mechanics." His ideas led to the theory of chaos. The full solution for three bodies was found in 1912 by Karl F. Sundman.

A computer simulation showing chaotic motion in the three-body problem.

Work on Relativity

Marie Curie and Poincaré talking at the 1911 Solvay Conference.

Poincaré's work on setting up international time zones made him think about how clocks would work if they were moving. At the same time, Hendrik Lorentz was developing a theory about how charged particles move and interact with light.

Local Time

In 1895, Lorentz introduced "local time," which was a mathematical idea. He also suggested that objects might shrink in length when moving (called length contraction). This helped explain why experiments couldn't detect motion through a special "aether" that was thought to fill space.

Poincaré was very interested in Lorentz's theory. He thought about its "deeper meaning." In 1898, he wrote that ideas about time only make sense if we agree on certain rules. He also said that scientists should assume the speed of light is constant. This makes physical theories simpler. In 1900, he talked about Lorentz's "wonderful invention" of local time. He noted that it came from clocks being synchronized by light signals, assuming light travels at the same speed in all directions.

Principle of Relativity and Lorentz Transformations

In 1881, Poincaré described hyperbolic geometry. He found transformations that kept certain measurements the same, which were mathematically like the Lorentz transformations.

In 1892, Poincaré developed a mathematical theory of light, including how light waves can be polarized. His way of showing how polarizers work, using a sphere, is called the Poincaré sphere. It was later shown that this sphere is related to Lorentz transformations.

In 1900, he discussed the "principle of relative motion." In 1904, he named it the principle of relativity. This principle states that no physical experiment can tell the difference between something moving at a steady speed and something staying still.

In 1905, Poincaré wrote to Lorentz about a paper Lorentz had published. Poincaré found a small error in Lorentz's work and questioned his idea of time slowing down (time dilation). In another letter, Poincaré explained why Lorentz's time dilation was correct. It was needed to make the Lorentz transformation work as a mathematical "group." He also gave what is now known as the relativistic velocity-addition law.

Poincaré later presented these ideas at a meeting in Paris in June 1905. He showed that a certain combination of space and time measurements stays the same during a Lorentz transformation. He also noted that a Lorentz transformation is like a rotation in a four-dimensional space. However, he didn't think it was worth the effort to rewrite all of physics in this four-dimensional way. It was Hermann Minkowski who later developed this idea further.

Mass–Energy Relation

Poincaré (1900) found a link between mass and electromagnetic energy. He was studying how Newton's action/reaction principle fit with Lorentz's theory. He realized that the electromagnetic field itself carries momentum.

Poincaré suggested that the energy of an electromagnetic wave acts like a fake fluid with a mass density of E/c² (where E is energy and c is the speed of light). He thought that if this fake fluid's mass was included, then the center of mass would still move at a steady speed. He also thought that electromagnetic energy could change into other forms of energy. To keep things balanced, he imagined another energy fluid that also carried mass. He called these ideas "mathematical fictions."

However, Poincaré's idea led to a problem when changing between different frames of reference. If a device sent out electromagnetic waves, it would recoil. Poincaré realized that this would mean the law of conservation of momentum was broken. This would allow for perpetual motion, which he knew was impossible. He thought there must be another way to balance things out in the "aether."

Albert Einstein's idea of mass–energy equivalence (1905) solved Poincaré's problem. Einstein showed that a body losing energy also loses mass (m = E/c²). This meant that the device sending out waves would lose mass, and momentum would still be conserved.

Gravitational Waves

In 1905, Poincaré was the first to suggest the existence of gravitational waves. He proposed that these waves would come from a body and travel at the speed of light.

Poincaré and Einstein

Einstein's first paper on relativity came out three months after Poincaré's shorter paper. Einstein used the principle of relativity to get the Lorentz transformations. He also used a similar way to synchronize clocks, like Poincaré had described. However, Einstein's paper did not mention any other works. Poincaré never publicly recognized Einstein's work on special relativity.

Einstein, however, did acknowledge Poincaré later. In 1921, he mentioned Poincaré in connection with non-Euclidean geometry. A few years before he died, Einstein said that Poincaré was one of the pioneers of relativity. He noted that Lorentz had found the transformations, and "Poincaré deepened this insight still further."

Views on Poincaré and Relativity

Poincaré's role in developing special relativity is well known. Most historians agree that while their work had similarities, Poincaré and Einstein had different goals. Poincaré used the idea of "local time" and saw its link to the speed of signals. But he still used the idea of the "aether" and believed that clocks at rest in the aether showed the "true" time. Einstein, on the other hand, created a new way of thinking about space and time, where they are relative.

While this is the common view, some historians, like E. T. Whittaker, believed that Poincaré and Lorentz were the true discoverers of relativity.

Algebra and Number Theory

Poincaré brought group theory into physics. He was the first to study the group of Lorentz transformations. He also made important contributions to the study of discrete groups.

Topology

A mug transforming into a torus, showing a topological change.

The title page of volume I of Les Méthodes Nouvelles de la Mécanique Céleste (1892).

Topology is a field of math that studies the properties of shapes that stay the same even when the shape is stretched or bent. The term "topology" was introduced by Johann Benedict Listing. Poincaré helped create the foundation of this science for spaces of any dimension. His first article on this topic was in 1894.

His work in geometry led to the abstract definitions of homotopy and homology. He also introduced basic ideas in combinatorial topology, like Betti numbers and the fundamental group. Poincaré proved a formula that connects the number of edges, vertices, and faces of an n-dimensional polyhedron. This is called the Euler–Poincaré theorem. He also gave the first clear definition of what "dimension" means.

Astronomy and Celestial Mechanics

Poincaré wrote two important books, "New Methods of Celestial Mechanics" (1892–1899) and "Lectures on Celestial Mechanics" (1905–1910). In these books, he used his research to study the motion of three bodies in space. He looked closely at how solutions behaved, including their frequency and stability.

He showed that the three-body problem cannot be solved in a simple, exact way. His work in this area was the first major step forward in celestial mechanics since Isaac Newton.

These books also included an idea that later became the basis for mathematical "chaos theory." This includes the Poincaré recurrence theorem, which says that certain systems will eventually return to a state very close to their starting point.

Poincaré also wrote important works on how rotating fluids balance themselves. He introduced the idea of bifurcation points. He showed that there are stable shapes for rotating fluids that are not simple spheres, like ring-shaped or pear-shaped figures. For this discovery, he received the Gold Medal of the Royal Astronomical Society in 1900.

Differential Equations and Mathematical Physics

After finishing his doctorate, Poincaré wrote a series of papers called "On curves defined by differential equations" (1881–1882). In these papers, he created a new area of math called "qualitative theory of differential equations."

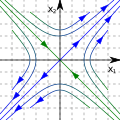
Poincaré showed that even if you can't solve a differential equation with known functions, you can still learn a lot about its properties. He studied how the paths of these equations behave. He classified different types of special points (like saddle points or focus points). He also introduced the idea of a limit cycle, which is a closed path that solutions can approach.

Poincaré applied these ideas to real-world problems in mathematical physics and celestial mechanics. His methods became the foundation for his later work in topology.

• The singular points of the integral curves
• 

  Saddle

• 

  Focus

• 

  Center 

• 

  Node

Henri Poincaré's Character

A photo of H. Poincaré by Henri Manuel.

Poincaré's work habits were compared to a bee flying from flower to flower. He was interested in how his own mind worked. In 1908, he gave a talk about his observations. He connected his way of thinking to how he made his discoveries.

The mathematician Darboux said Poincaré was "intuitive." This means he often worked by visualizing things. Jacques Hadamard wrote that Poincaré's research was very clear. Poincaré himself believed that logic helped structure ideas, but it wasn't how new ideas were invented.

How Toulouse Described Him

A psychologist named Édouard Toulouse studied Poincaré's mental organization. Toulouse wrote a book about Henri Poincaré in 1910. In it, he described Poincaré's daily routine:

• He worked at the same times each day for short periods. He did math research for four hours a day.
• He usually solved problems completely in his head before writing them down.
• He was ambidextrous (could use both hands well) and nearsighted.
• His ability to visualize what he heard was very helpful in lectures, since he couldn't see the blackboard well.

However, he also had some weaknesses:

• He was physically clumsy and not good at art.
• He was always in a hurry and didn't like to go back and make changes.
• He never spent too long on one problem. He believed his subconscious mind would keep working on it while he focused on something else.

Toulouse also noted that most mathematicians worked from existing rules, but Poincaré often started from basic principles each time.

Honors and Awards

Awards

• Oscar II, King of Sweden's mathematical competition (1887)
• Foreign member of the Royal Netherlands Academy of Arts and Sciences (1897)
• American Philosophical Society (1899)
• Gold Medal of the Royal Astronomical Society of London (1900)
• Bolyai Prize (1905)
• Matteucci Medal (1905)
• French Academy of Sciences (1906)
• Académie française (1909)
• Bruce Medal (1911)

Things Named After Him

• Institut Henri Poincaré (a math and physics center)
• Poincaré Prize (an international math physics award)
• Annales Henri Poincaré (a science journal)
• The crater Poincaré on the Moon
• Asteroid 2021 Poincaré
• List of things named after Henri Poincaré

Henri Poincaré did not win the Nobel Prize in Physics. However, he was nominated 51 times between 1904 and 1912. Many famous scientists, including Nobel winners like Marie Curie and Hendrik Lorentz, nominated him.

Some people think that the Nobel committee valued experiments more than theory. In Poincaré's case, it was hard to name one specific discovery or invention for the prize.

His Philosophy

The first page of Science and hypothesis (1905).

Poincaré had different philosophical ideas than Bertrand Russell and Gottlob Frege. They believed that mathematics was a part of logic. Poincaré strongly disagreed, saying that intuition was the most important part of mathematics.

Poincaré believed that arithmetic (basic math) is "synthetic." He argued that certain math rules cannot be proven without using the same rules. He concluded that math cannot be fully based on logic. His ideas were similar to those of Immanuel Kant. He also strongly disliked Cantor's set theory.

However, Poincaré didn't agree with Kant on everything. For example, in geometry, Poincaré thought that the structure of non-Euclidean space could be understood through analysis.

Poincaré believed that agreements or "conventions" play a big role in physics. This idea is called "conventionalism." He thought that Newton's first law was not just a fact, but a basic assumption we agree on for mechanics. He also thought that the geometry of physical space is a convention. He gave examples where we could either describe space as non-Euclidean or change physical laws to keep it Euclidean. Poincaré thought we would prefer to keep Euclidean geometry and change the physical laws instead.

Free Will and Creativity

Poincaré gave famous lectures where he discussed how the creativity and invention process works. He suggested it has two stages: first, the mind randomly combines possible solutions to a problem. Second, it then carefully evaluates these combinations.

Even though he often spoke about a deterministic universe (where everything is decided), Poincaré said that the subconscious mind's generation of new possibilities involves chance.

Poincaré's two stages of random combinations followed by selection became the basis for Daniel Dennett's model of free will.

See also

In Spanish: Henri Poincaré para niños

Concepts

Theorems

Here is a list of theorems proved by Poincaré:

Other

Images for kids

• 

  The Poincaré family grave at the Cimetière du Montparnasse.