Fundamental group facts for kids
The fundamental group is a cool idea in mathematics, especially in a field called algebraic topology. Imagine a shape, like a donut or a sphere. The fundamental group helps us understand the "holes" or basic shape of that object.
It does this by looking at all the loops you can draw on the shape that start and end at the same point. Two loops are considered the same if you can smoothly change one into the other without breaking it or leaving the shape. The fundamental group is like a special collection (a group) of all these different kinds of loops. It's the first and simplest way to describe a shape's "holey-ness."
If two shapes are similar enough (we call this homotopy equivalent or homeomorphic), they will have the same fundamental group. We write the fundamental group of a shape X as 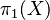 .
.
Contents
What is a Fundamental Group?
Imagine you have a surface, like a donut. Pick a starting point on it. Now, think about all the paths that start at this point, wander around, and then come back to the exact same starting point. These are called loops.
You can combine two loops: just travel along the first loop, then immediately travel along the second.
Two loops are thought of as "the same" if you can smoothly change one into the other without tearing the surface or lifting the loop off it. The collection of all these different kinds of loops, with this way of combining them, forms the fundamental group for that specific shape.
History of the Idea
The idea of the fundamental group was first introduced by a mathematician named Henri Poincaré in 1895. He wrote about it in his paper "Analysis situs".
This concept grew out of studies of Riemann surfaces by mathematicians like Bernhard Riemann, Poincaré, and Felix Klein. It helped describe how complex functions behave and also helped classify different types of closed surfaces.
How We Define It
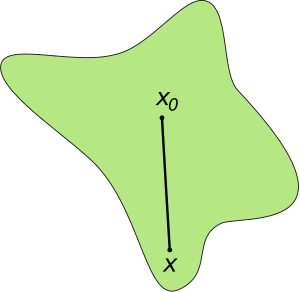
Let's think about a shape, which we'll call X. A good example is a surface like the one shown on the right. We also pick a special point in X called the base-point, usually written as 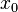 . This point helps us define the loops.
. This point helps us define the loops.
The main idea is to measure how many different kinds of curves on X can be smoothly changed into each other.
Loops and Homotopy
A loop starting at 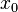 is a continuous path that begins at
is a continuous path that begins at 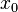 and ends back at
and ends back at 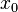 . Think of it as drawing a continuous line that forms a closed circle.
. Think of it as drawing a continuous line that forms a closed circle.
A homotopy is like a smooth transformation between two loops. Imagine you have two loops, 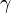 and
and 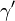 , that both start and end at
, that both start and end at 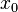 . A homotopy is a way to continuously morph
. A homotopy is a way to continuously morph 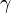 into
into 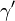 without ever lifting the loop off the surface or changing its start/end point.
without ever lifting the loop off the surface or changing its start/end point.
If such a smooth transformation exists, we say 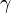 and
and 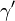 are homotopic. This relationship lets us group loops into equivalence classes. All loops in one class can be smoothly deformed into each other.
are homotopic. This relationship lets us group loops into equivalence classes. All loops in one class can be smoothly deformed into each other.
The fundamental group 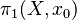 is the collection of all these equivalence classes of loops.
is the collection of all these equivalence classes of loops.
How Loops Form a Group
The fundamental group isn't just a collection of loop classes; it's a group. This means we can "multiply" or combine loop classes.
If you have two loops, 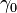 and
and 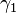 , you can combine them to make a new loop. First, you travel along
, you can combine them to make a new loop. First, you travel along 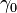 , and then you travel along
, and then you travel along 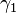 . We make sure this new combined loop also starts and ends at
. We make sure this new combined loop also starts and ends at 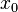 .
.
This way of combining loops works for their equivalence classes too. The "identity element" of the group is a loop that just stays at the base point 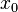 the whole time. The "inverse" of a loop is the same loop, but traveled in the opposite direction.
the whole time. The "inverse" of a loop is the same loop, but traveled in the opposite direction.
Because we consider loops "up to homotopy" (meaning we allow smooth deformations), this combination rule makes the collection of loop classes a true mathematical group.
Does the Starting Point Matter?
The fundamental group technically depends on the chosen base point 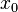 . However, if the shape X is path-connected (meaning you can draw a continuous path between any two points in the shape), then the fundamental group will be the same no matter which base point you choose. Because of this, many people just write
. However, if the shape X is path-connected (meaning you can draw a continuous path between any two points in the shape), then the fundamental group will be the same no matter which base point you choose. Because of this, many people just write 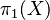 without mentioning the base point.
without mentioning the base point.
Examples of Fundamental Groups
Flat Spaces
In a flat space, like a flat plane (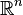 ) or any bowl-shaped area, any loop can be shrunk down to a single point. This means there's only one type of loop (the one that shrinks to a point). So, the fundamental group of such spaces is the trivial group, which has only one element.
) or any bowl-shaped area, any loop can be shrunk down to a single point. This means there's only one type of loop (the one that shrinks to a point). So, the fundamental group of such spaces is the trivial group, which has only one element.
A space where every loop can be shrunk to a point is called simply connected.
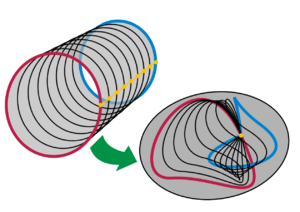
The 2-Sphere (Surface of a Ball)

The surface of a ball, called the 2-sphere (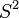 ), is simply connected. This means its fundamental group is also trivial. You can imagine any loop drawn on a ball's surface can be smoothly shrunk down to a single point, as shown in the picture.
), is simply connected. This means its fundamental group is also trivial. You can imagine any loop drawn on a ball's surface can be smoothly shrunk down to a single point, as shown in the picture.
The Circle
The circle (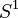 ) is different. It's not simply connected because it has a "hole" in the middle.
) is different. It's not simply connected because it has a "hole" in the middle.
Imagine loops on a circle. Some loops go around the circle once, some twice, some three times, and so on. They can also go in the opposite direction (negative winding).
If you combine a loop that goes around m times with a loop that goes around n times, you get a loop that goes around m + n times. This is just like adding integers! So, the fundamental group of the circle is like the group of integers with addition, written as 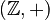 .
.
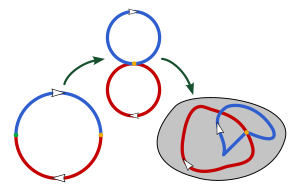
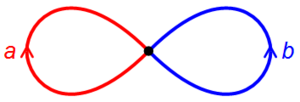
The Figure Eight
The figure eight shape is made of two circles joined at a point. Its fundamental group is called a free group on two "letters."
If you pick the meeting point as the base point, any loop on the figure eight can be described by going around one circle (let's call it 'a') or the other (let's call it 'b'), multiple times and in different directions.
Unlike the circle's fundamental group, the figure eight's group is not abelian. This means that going around circle 'a' then 'b' is not the same as going around 'b' then 'a' (they can't be smoothly deformed into each other).
Graphs
The fundamental group can also be found for graphs (like networks of points and lines). For a connected graph, its fundamental group is always a free group. The number of "generators" (the basic loops) is equal to the number of edges you have to add to a spanning tree to get the original graph. This number is calculated as: (number of edges) - (number of vertices) + 1.
For example, a grid-like graph with 16 vertices and 24 edges would have a fundamental group that is a free group with 9 generators. This makes sense because the graph has 9 "holes" or enclosed regions.
Knot Groups
Knot groups are the fundamental groups of the space around a knot in 3D space. For example, the knot group of the trefoil knot (a common three-leaf knot) is a special group called the braid group 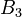 . This is another example of a fundamental group that is not abelian.
. This is another example of a fundamental group that is not abelian.
Knot groups are used in knot theory to tell different knots apart. If two knots have different knot groups, then you can't smoothly transform one into the other. For instance, a trefoil knot cannot be turned into a simple circle (called the unknot) because the unknot's group is 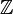 , which is different from the trefoil's group.
, which is different from the trefoil's group.
Oriented Surfaces
For a surface with n "handles" (called genus-n orientable surface), the fundamental group can be described using generators and relations.
For example, a torus (a donut shape) has genus 1. Its fundamental group is like 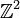 , which means it's similar to pairs of integers
, which means it's similar to pairs of integers 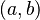 where you add them like
where you add them like 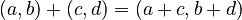 . This group is abelian.
. This group is abelian.
How Fundamental Groups Behave
Relationship to Homology
The fundamental group can be complex because it might not be abelian (the order of combining loops matters). However, there's a related concept called the homology group (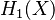 ) which is always abelian.
) which is always abelian.
There's a special connection: the first homology group is like the "abelianized" version of the fundamental group. This means that if you take the fundamental group and force it to be abelian, you get the first homology group.
Gluing Shapes Together
A powerful tool for calculating fundamental groups is the Seifert–van Kampen theorem. This theorem helps us find the fundamental group of a shape that is made by "gluing" two or more simpler shapes together.
For example, a 2-sphere (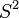 ) can be thought of as two slightly overlapping half-spheres glued along their "equator." Since each half-sphere is simply connected (its fundamental group is trivial), the theorem helps us see that the fundamental group of the whole sphere is also trivial.
) can be thought of as two slightly overlapping half-spheres glued along their "equator." Since each half-sphere is simply connected (its fundamental group is trivial), the theorem helps us see that the fundamental group of the whole sphere is also trivial.
Coverings
Imagine a "covering" of a shape B by another shape E. This is like having a sheet E that lays over B in a special way, so that if you look at a small part of B, the part of E above it looks like several separate copies of that small part.
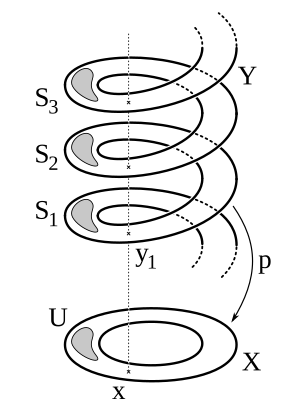
Universal Covering
A special kind of covering is called a universal covering. In this case, the covering space E is simply connected (meaning it has no "holes" and its fundamental group is trivial).
Knowing the universal covering of a space X helps us understand its fundamental group. The fundamental group of X can be identified with the "deck transformations" of the universal covering. These are special transformations of the covering space that don't change how it lays over X.
For example, the real number line (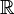 ) is a universal covering of the circle (
) is a universal covering of the circle (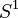 ). The "deck transformations" are like adding any integer to a point on the number line. This matches our earlier finding that the fundamental group of the circle is like the integers (
). The "deck transformations" are like adding any integer to a point on the number line. This matches our earlier finding that the fundamental group of the circle is like the integers (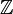 ).
).
If a simply connected space Y is acted upon by a discrete group G (like a group of symmetries), then the fundamental group of the resulting shape 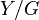 is often just G itself. For example, the real projective space
is often just G itself. For example, the real projective space 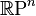 has a fundamental group of
has a fundamental group of 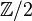 for dimensions 2 or higher.
for dimensions 2 or higher.
Lie Groups
Lie groups are special kinds of groups that are also smooth shapes. The fundamental group of a connected, simply connected compact Lie group (like 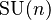 ) is always trivial. This means these groups are simply connected.
) is always trivial. This means these groups are simply connected.
For example, the special unitary group 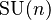 for
for 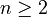 is simply connected. This can be shown by breaking down the problem using a technique called "fibration sequences."
is simply connected. This can be shown by breaking down the problem using a technique called "fibration sequences."
Here are some results for the fundamental groups of some important Lie groups:
| Compact Lie group G | Non-compact Lie group | 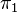 |
|---|---|---|
special unitary group 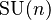 |
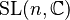 |
1 (trivial group) |
unitary group 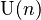 |
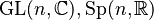 |
 (integers) (integers) |
special orthogonal group 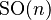 |
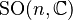 |
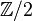 for for 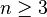 and and 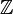 for for  |
compact symplectic group 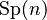 |
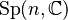 |
1 (trivial group) |
Edge-Path Group of a Simplicial Complex
When a shape is like a simplicial complex (made of points, lines, and triangles glued together), its fundamental group can be described using "edge-paths."
An edge-path is a chain of vertices connected by edges. An edge-loop starts and ends at the same vertex. The edge-path group is made of these edge-loops, where two loops are the same if you can transform one into the other by using the triangles in the complex.
This edge-path group is exactly the same as the fundamental group of the simplicial complex. This method is often used to calculate fundamental groups and shows that many different kinds of groups can be fundamental groups of shapes.
What Can Be a Fundamental Group?
- Any group can be the fundamental group of a CW-complex (a type of shape built from simple pieces) that has at least two dimensions. However, for 1-dimensional shapes (like graphs), only free groups can be fundamental groups.
- Any finitely presented group (a group described by a finite number of generators and relations) can be the fundamental group of a smooth, connected manifold of dimension 4 or higher.
Related Ideas
Higher Homotopy Groups
The fundamental group helps us find 1-dimensional "holes." But shapes can have "holes" in higher dimensions too, like the empty space inside a 2-sphere. Higher homotopy groups (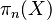 ) are used to detect these. They are defined using maps from higher-dimensional spheres (
) are used to detect these. They are defined using maps from higher-dimensional spheres (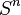 ) to the shape X. For example, the n-th homotopy group of the n-sphere is
) to the shape X. For example, the n-th homotopy group of the n-sphere is 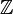 .
.
Loop Space
The collection of all loops (not just their equivalence classes) in a shape X is called the loop space, written as  . The fundamental group of X is related to the "connected pieces" of its loop space.
. The fundamental group of X is related to the "connected pieces" of its loop space.
Fundamental Groupoid
The fundamental groupoid is a more general idea than the fundamental group. It's useful when you don't want to pick a single base point. Instead of just loops, it considers all paths between any two points in the shape.
See also
 In Spanish: Grupo fundamental para niños
In Spanish: Grupo fundamental para niños





![\mathbb{R} \times [0,1] \to S^1 \times [0,1]](/images/math/5/d/7/5d72ba3b0e2aa028422bb575fc41f59a.png) is a covering. The space
is a covering. The space ![\mathbb{R} \times [0,1]](/images/math/e/c/b/ecb6ddefe9871a4a5aa9a403ac38347e.png) is simply connected, making it a universal covering.
is simply connected, making it a universal covering.