Riemann surface facts for kids

This picture shows a Riemann surface for the square root function. It helps us see how the function works for different complex numbers.

In mathematics, especially in a field called complex analysis, a Riemann surface is a special kind of surface. Think of it as a connected, one-dimensional shape in a complex number world. These surfaces were first studied by a mathematician named Bernhard Riemann, and they are named after him.

Riemann surfaces can be imagined as squished or stretched versions of the regular complex plane (which is like a flat map for complex numbers). If you look very closely at any part of a Riemann surface, it will look like a small piece of the complex plane. But when you look at the whole surface, its overall shape can be very different. For example, it might look like a sphere, a torus (a donut shape), or even several sheets of paper glued together.

Mathematicians are interested in Riemann surfaces because they are the perfect place to study special types of functions called holomorphic functions. These surfaces are especially helpful for understanding functions that can have many different answers, like the square root (a number can have two square roots, like 4 has 2 and -2) or the logarithm.

Every Riemann surface is also a two-dimensional real surface, but it has an extra "complex structure." This extra structure is what allows mathematicians to clearly define and study holomorphic functions.

What Are Riemann Surfaces Like?

A Riemann surface is a bit like a map of the Earth. If you look at a small part of the Earth, it seems flat, like a map. But the whole Earth is a sphere. Riemann surfaces are similar:

• Local View: Close up, any spot on a Riemann surface looks just like a flat piece of the complex plane.
• Global View: The entire surface can have a much more interesting shape, like a sphere or a donut.

This idea of "local flatness" but "global curvature" is key to understanding them.

Why Are Riemann Surfaces Important?

Riemann surfaces are super useful for studying functions that involve complex numbers. Imagine a function like the square root of a complex number. For most numbers, there are two possible square roots. How do you draw that on a simple graph? It gets complicated!

Riemann surfaces provide a way to "unfold" these multi-valued functions onto a single surface. This makes it much easier to see how these functions behave and to understand all their possible answers in a smooth way. They are the natural home for these kinds of functions.

How Are Riemann Surfaces Defined?

Mathematicians define a Riemann surface in a very precise way. One common way to think about it is:

• It's a connected space (you can get from any point to any other point without leaving the surface).
• It's a Hausdorff space (different points can be separated).
• It has "charts" that map small parts of the surface to the open unit disk in the complex plane. Think of these charts like map sections.
• When these map sections overlap, the way they connect (called "transition maps") must be "holomorphic." This means the connections are very smooth and preserve the complex structure.

Another way to define a Riemann surface is as a two-sided surface (like a piece of paper, not a Möbius strip) that has a "conformal structure." This means you can measure angles on the surface, and these angle measurements are preserved even if the surface is stretched or bent.

Cool Examples of Riemann Surfaces

The Riemann sphere is like the complex plane wrapped around a ball.

A torus, or donut shape, can also be a Riemann surface.

Here are some examples to help you picture them:

• The Complex Plane: The most basic Riemann surface is the entire complex plane itself. It's just a flat, infinite surface where every point is a complex number.
• Parts of the Complex Plane: Any non-empty open subset (a piece without its edges) of the complex plane can also be a Riemann surface.
• The Riemann Sphere: Imagine taking the complex plane and wrapping it around a sphere. You add one extra point, called "infinity," at the very top of the sphere. This creates the Riemann sphere. It's a very important example because, unlike the flat complex plane, it's a compact surface (it doesn't go on forever).
• Tori (Donut Shapes): A torus (the shape of a donut) can also be a Riemann surface. You can create a torus by taking a rectangle in the complex plane and gluing its opposite sides together. These are special because they are the only Riemann surfaces that have a "genus" of one (meaning they have one "hole").
• Hyperelliptic Surfaces: Surfaces with more holes (higher "genus") can be created using more complex equations. For example, surfaces with two or more holes are called hyperelliptic surfaces.

• 

  This shows the Riemann surface for the arcsin function.

• 

  This is the Riemann surface for the logarithm function.

• 

  This is the Riemann surface for the square root function, z^1/2.

• 

  This shows the Riemann surface for the cube root function, z^1/3.

• 

  This is the Riemann surface for the fourth root function, z^1/4.

How Riemann Surfaces Are Classified

Riemann surfaces can be grouped into three main types based on their overall shape and how they curve:

• Elliptic: These are like the Riemann sphere. They have a positive curvature, like the outside of a ball.
• Parabolic: These are like the complex plane or a cylinder. They have zero curvature, like a flat sheet of paper.
• Hyperbolic: These are the most common type for surfaces with many holes. They have negative curvature, like a saddle.

This classification is based on something called the uniformization theorem, which says that every simple Riemann surface is like one of these three basic shapes.

Elliptic Riemann Surfaces

The Riemann sphere is the only example of an elliptic Riemann surface. It's like a perfect ball.

Parabolic Riemann Surfaces

If a Riemann surface is "parabolic," it means its basic shape is like the complex plane. Examples include:

• The complex plane itself.
• A cylinder (which you can get by taking the complex plane and identifying points that are a certain distance apart).
• A torus (a donut shape). Even though tori have a hole, they are considered parabolic in this classification.

Hyperbolic Riemann Surfaces

Most Riemann surfaces are "hyperbolic." This includes any surface that is not a sphere, a plane, a cylinder, or a torus. For example, a surface with two or more holes will be hyperbolic.

Maps Between Riemann Surfaces

Just like you can have functions that map numbers to other numbers, you can have special functions (called holomorphic maps) that map points from one Riemann surface to another.

• It's easy to map from a "hyperbolic" surface to a "parabolic" one, or from a "parabolic" one to an "elliptic" one.
• But it's very hard to map in the other direction! For example, you can't have a non-constant holomorphic map from a sphere to a plane. This is because of special theorems like Liouville's theorem.

Punctured Spheres

Let's look at the Riemann sphere again, but with some "punctures" (holes):

• No punctures: It's the Riemann sphere, which is elliptic.
• One puncture: If you remove one point (say, the "infinity" point), you get the complex plane, which is parabolic.
• Two punctures: If you remove two points, you get a shape like a cylinder or an annulus (a ring), which is also parabolic.
• Three or more punctures: If you remove three or more points, the surface becomes hyperbolic.

This shows how adding or removing just a few points can completely change the type of a Riemann surface!

Ramified Covering Spaces

When you have a non-constant holomorphic map between compact Riemann surfaces, it acts like a "ramified covering map." Imagine one surface laying over another, with some points "branching" or overlapping.

For example, hyperbolic Riemann surfaces can "cover" the sphere (meaning you can map them onto the sphere in a special way). But a sphere cannot cover a surface with more holes, unless the map is just a constant (meaning every point on the sphere maps to just one single point on the other surface). This is explained by a formula called the Riemann–Hurwitz formula.

Images for kids

• 

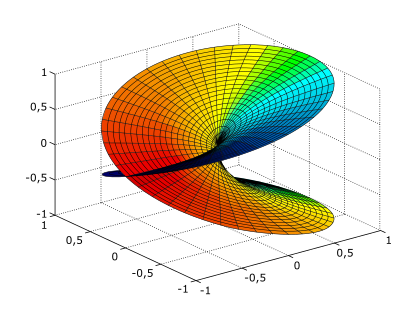
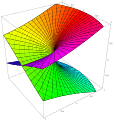
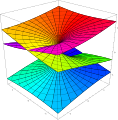
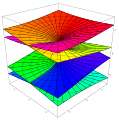
  Riemann surface for the function f(z) = √z. The two horizontal axes represent the real and imaginary parts of z, while the vertical axis represents the real part of √z. The imaginary part of √z is represented by the coloration of the points. For this function, it is also the height after rotating the plot 180° around the vertical axis.

• 

  The Riemann sphere.

• 

  A torus.