Holomorphic function facts for kids
A holomorphic function is a special kind of function used in mathematics. It works with complex numbers instead of just regular numbers. Imagine complex numbers as points on a flat surface, not just on a line.
A holomorphic function is "smooth" and "well-behaved" everywhere it's defined. This means you can find its "slope" or "rate of change" (which mathematicians call a derivative) at any point within its area. Even better, you can keep finding the derivative again and again, and it will always be a holomorphic function too!
In older math books, these functions were sometimes called regular functions. Holomorphic functions have many unique features that functions working only with regular numbers (called real numbers) do not have.
Contents
What is a Function?
In math, a function is like a machine that takes an input and gives you an output. For example, if you have a function that doubles a number, you put in 5, and it gives you 10.
Inputs and Outputs
- Input: The number or value you put into the function.
- Output: The number or value the function gives back.
- Rule: Every function has a rule that tells it how to change the input into the output.
Understanding Complex Numbers
To understand holomorphic functions, you first need to know about complex numbers.
What are Complex Numbers?
Complex numbers are numbers that have two parts:
- A real part (like the numbers you use every day: 1, 5, -10).
- An imaginary part (which involves the special number i, where i is defined as the square root of -1).
You can think of a complex number like a point on a map. The real part tells you how far to go left or right, and the imaginary part tells you how far to go up or down.
What Does "Differentiable" Mean?
When a function is "differentiable," it means you can find its slope or rate of change at any point.
Finding the Slope
Imagine drawing a graph of a function. If you can draw a smooth line that just touches the graph at any point without suddenly jumping or having sharp corners, then the function is differentiable at that point. For holomorphic functions, this is true for every point where the function is defined.
Special Properties of Holomorphic Functions
Holomorphic functions are very powerful and have amazing properties that make them unique.
Smooth and Predictable
- Infinitely Differentiable: Unlike some functions with real numbers, if a function is holomorphic, you can find its derivative an endless number of times. Each new derivative will also be a holomorphic function.
- Analytic: This means that a holomorphic function can be perfectly described by a special kind of infinite sum called a Taylor series. This is like saying you can predict its behavior perfectly just by knowing what it does at one point.
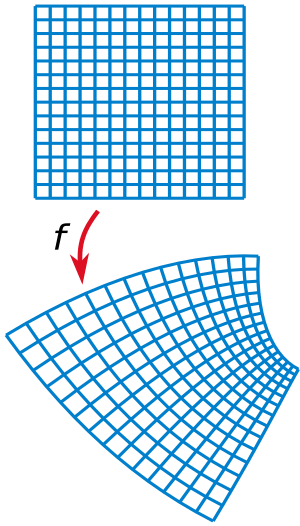
Angle-Preserving Maps
- Conformal Mapping: Holomorphic functions have a cool property called "conformal mapping." This means that if you draw two lines that cross at a certain angle, and then you apply a holomorphic function to these lines, the new lines will still cross at the exact same angle. This is very useful in areas like map-making or designing airplane wings.
Maximum Modulus Principle
- No Local Peaks: For a holomorphic function, its largest value (or "magnitude") within a certain area must always happen on the edge of that area, not in the middle. It's like saying the highest point of a hill can't be in the middle of a flat field; it has to be on the boundary of the field.
Where Are Holomorphic Functions Used?
Holomorphic functions are not just abstract math ideas; they are used in many real-world applications.
Engineering and Physics
- Fluid Dynamics: They help scientists understand how fluids (like water or air) flow.
- Electrical Engineering: They are important in designing electrical circuits and analyzing signals.
- Quantum Mechanics: These functions are also used in the study of very small particles and their behavior.
Other Fields
- Computer Graphics: They can be used to create complex shapes and transformations in computer graphics.
- Control Theory: This field uses holomorphic functions to design systems that can control other systems, like robots or automated factories.
Holomorphic functions are a cornerstone of advanced mathematics and provide powerful tools for solving problems in many different areas of science and engineering.
See also
 In Spanish: Función holomorfa para niños
In Spanish: Función holomorfa para niños