Riemann sphere facts for kids
The Riemann sphere is a special way to think about complex numbers. Imagine all the complex numbers, which usually live on a flat plane, plus one extra point called "infinity." The Riemann sphere helps us see all these numbers, including infinity, as points on the surface of a sphere.
This idea is named after a famous mathematician, Bernhard Riemann. It's super helpful in a part of math called Complex analysis. For example, when you divide a number by zero, it usually doesn't make sense. But with the Riemann sphere, dividing by zero can lead you to that "infinity" point, which makes some math problems easier to understand and solve. It also helps make certain mathematical functions "continuous," meaning they flow smoothly without any sudden jumps or breaks.
In geometry, the Riemann sphere is a simple example of a Riemann surface. It's also one of the easiest complex manifolds to understand.
Contents
What is a Complex Number?
To understand the Riemann sphere, let's quickly talk about complex numbers. You know regular numbers like 1, 2, 3, or -5. These are called "real numbers." Complex numbers are a bit different because they include the imaginary number i, where i is defined as the square root of -1.
A complex number usually looks like a + bi, where 'a' and 'b' are real numbers. You can think of them as points on a 2D plane, where 'a' is the x-coordinate and 'b' is the y-coordinate.
Adding the Point at Infinity
The big idea behind the Riemann sphere is adding a "point at infinity" to the regular complex plane. Think of it like this: as numbers get bigger and bigger, they get "closer" to this infinity point. It's similar to how numbers very close to zero (like 0.0001 or -0.0001) are "close" to zero itself.
This point at infinity helps make certain mathematical operations, like division by zero, behave in a more predictable way.
How Does it Work? Stereographic Projection
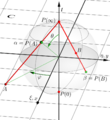
The way we connect the flat complex plane to the round sphere is through something called stereographic projection. Imagine a sphere sitting on top of the complex plane, touching it at the "south pole." Now, imagine a light source at the "north pole" of the sphere.
If you have a point on the complex plane, you can draw a straight line from the north pole through that point on the plane until it hits the sphere. Where it hits the sphere is the "image" of that complex number on the sphere.
- Numbers close to the center of the plane (the origin) will map to points near the south pole of the sphere.
- Numbers far away from the center of the plane (very large numbers) will map to points closer to the north pole.
- The "point at infinity" on the complex plane is exactly where the north pole of the sphere is.
This projection creates a perfect match between every point on the complex plane (plus infinity) and every point on the sphere.
Why is the Riemann Sphere Useful?
The Riemann sphere is useful for a few reasons:
- Simplifies math: It helps mathematicians study functions that might have "singularities" (points where they don't behave well, like division by zero). By mapping these functions to the sphere, they can become smoother and easier to analyze.
- Visualizing complex functions: It provides a great way to visualize how complex functions transform the complex plane.
- Geometry: It's a fundamental example in higher-level geometry, like Riemann surfaces and complex manifolds, which are important in advanced mathematics and physics.
Images for kids
-
Stereographic projection of a complex number A onto a point α of the Riemann sphere
-
A Möbius transformation acting on the sphere, and on the plane by stereographic projection
See also
In Spanish: Esfera de Riemann para niños
