Coriolis effect facts for kids

The Coriolis effect is like an invisible push or pull that happens on things moving across a spinning surface. Think of it as a trick of movement! It's not a real force you can feel directly, but it makes moving objects look like they are curving.
A French scientist named Gaspard-Gustave de Coriolis first explained this effect in 1835. He used math to show how it works.
You can see the Coriolis effect best in huge weather systems like hurricanes and typhoons. In the northern part of the world, these storms spin counter-clockwise. This is because the Earth itself spins counter-clockwise when you look down from the North Pole. In the southern part of the world, storms spin clockwise.
Many people think the Coriolis effect makes water go down a drain in different directions depending on where you are on Earth. However, this isn't true! The Coriolis effect is far too weak to be seen in a small sink or bathtub. Other things like the shape of the drain or how the water was poured make a much bigger difference.
Contents
How the Coriolis Effect Works
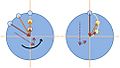
Imagine you are on a giant spinning merry-go-round. If you try to throw a ball straight across to a friend, it won't go straight! From your point of view on the merry-go-round, the ball will seem to curve. This is because while the ball is flying, you and your friend are also moving with the merry-go-round.
Spinning Earth and Air
The Earth is like a giant merry-go-round, always spinning. This spin affects anything that moves freely over long distances, like air currents or ocean currents.
- When air moves from the equator towards the North Pole, it seems to curve to the right.
- When air moves from the equator towards the South Pole, it seems to curve to the left.
This curving motion is what helps create the big swirling patterns of weather. It also affects things like rockets and airplanes on long flights.
Why Storms Spin
The Coriolis effect is super important for how big storms form and move.
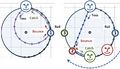
- In the Northern Hemisphere, air rushes towards a low-pressure area. As it moves, the Coriolis effect makes it curve to the right. This curving creates a counter-clockwise spin, forming hurricanes and other cyclones.
- In the Southern Hemisphere, the air curves to the left as it moves towards low pressure. This creates a clockwise spin for storms there.
Without the Coriolis effect, these massive storms wouldn't spin the way they do!
Images for kids
See also
 In Spanish: Efecto Coriolis para niños
In Spanish: Efecto Coriolis para niños