Difference quotient facts for kids

The difference quotient is a special math tool that helps us understand how things change. Imagine you're riding a roller coaster. Your speed isn't always the same, right? The difference quotient helps mathematicians figure out how fast something is changing at any exact moment, even on a curvy path. It's super important in a type of math called calculus. A famous scientist named Isaac Newton helped create this idea.

What is the Difference Quotient?

Finding the Slope of a Curve

You might know how to find the slope of a straight line. It's simply how much the line goes up or down (change in y) divided by how much it goes sideways (change in x). This works perfectly for straight lines.

But what if you have a curved line? How do you find its slope at a specific point? That's where the difference quotient comes in! It helps us find the slope of a curve, or how steep it is, at any single point.

The Math Behind It

The difference quotient is like a special version of the slope formula. It looks at two points on a curve that are very, very close to each other.

Here's the basic idea of the slope formula: 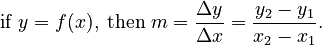Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathrm{if \;} y = f(x), \mathrm{\; then \;} m= \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1}.

For the difference quotient, we use a slightly different way to write the points. We imagine one point is at x, and the other is just a tiny bit away, at x plus a small change (we call this change 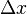or h).

So, the difference quotient formula looks like this: 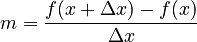Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): m = \frac{f(x + \Delta x) - f(x)}{\Delta x}

This formula helps us find the slope of a line that connects two points on a curve. This line is called a secant line.

From Difference Quotient to Derivative

The really cool part happens when those two points on the curve get closer and closer together. When they are almost on top of each other, the difference quotient gives us the exact slope of the curve at that single point.

This process of finding the exact slope at one point is called differentiation. The new function we get from this process is called the derivative. The derivative tells us the slope of the curve at any point we choose.

How We Use the Difference Quotient

The ideas from the difference quotient and the derivative are used in many real-world situations.

Physics and Speed

In physics, the derivative is super useful for understanding motion. For example, if you know a car's position at different times, you can use the derivative to find its exact speed at any moment. This is called its instantaneous velocity.

• If a car's position is described by a formula like x(t)=-16t²+16t+32, then its speed (velocity) at any time t is found by taking the derivative. In this case, the velocity formula would be v(t)=-32t+16.
• You can even find the car's acceleration (how fast its speed is changing) by taking the derivative of the velocity formula! For the example above, the acceleration would be a(t) = -32.

Related pages

• Partial derivative