Partial derivative facts for kids
A partial derivative is a special tool in calculus, which is an advanced part of mathematics. Imagine you have a recipe where the taste depends on how much sugar and how much salt you add. A partial derivative helps you understand how the taste changes if you only change the sugar, while keeping the salt exactly the same.
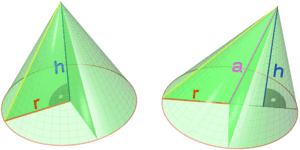
In math, a partial derivative tells us how a function changes when only one of its many inputs changes. All other inputs are kept steady. This is super useful when a function has two or more variables. For example, the volume of a cone depends on its height and the radius of its base. If you want to know how the volume changes only when the height changes (and the radius stays the same), you would use a partial derivative.
The special symbol for a partial derivative looks like this: 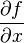 . It means we are looking at how the function f changes with respect to x, while treating all other variables as constants.
. It means we are looking at how the function f changes with respect to x, while treating all other variables as constants.
Contents
What is a Partial Derivative?
A partial derivative helps us study how complex things change. Think of a function as a rule that takes some numbers and gives you a new number. For example, a function might take x and y and give you z. If you want to know how z changes when x changes, but y stays fixed, that's where a partial derivative comes in. It's like focusing on just one ingredient in a recipe.
Understanding Variables
In math, a variable is a symbol, like x or y, that can stand for different numbers. When a function has more than one variable, it's called a multivariable function. For example, the area of a rectangle depends on its length and its width. Both length and width are variables.
When we take a partial derivative, we pick one variable to focus on. We pretend all the other variables are just fixed numbers, like 5 or 10. Then we find the derivative as usual for our chosen variable.
Real-World Examples
Partial derivatives are used in many fields. Scientists use them to understand how temperature changes across a room. Engineers use them to design cars or airplanes. They help predict how things will behave when multiple factors are at play.
Calculating Partial Derivatives
Let's look at an example to make it clearer. Imagine we have a function 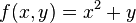 . This function takes an x value and a y value. It then squares x and adds y to it.
. This function takes an x value and a y value. It then squares x and adds y to it.
If we want to find the partial derivative with respect to y, we treat x as a constant number. So, for 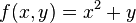 :
:
- The derivative of
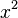 (which we treat as a constant) is 0.
(which we treat as a constant) is 0. - The derivative of
 is 1.
is 1.
So, the partial derivative with respect to y is:
Now, if we want to find the partial derivative with respect to x, we treat y as a constant number. So, for 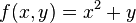 :
:
- The derivative of
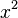 is
is 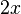 .
. - The derivative of
 (which we treat as a constant) is 0.
(which we treat as a constant) is 0.
So, the partial derivative with respect to x is:
This shows how we can look at the change caused by one variable at a time.
Related Topics
See also
 In Spanish: Derivada parcial para niños
In Spanish: Derivada parcial para niños


![\frac{\partial }{\partial y}[f(x, y)]=1](/images/math/e/1/a/e1aafeb463a64d27d91d940ad81e99c2.png)
![\frac{\partial}{\partial x}[f(x, y)]=2x](/images/math/4/1/4/414fa063347b99d2dbfdc13d8b59c285.png)