Divergent series facts for kids
In mathematics, imagine you're adding up an endless list of numbers. If this sum keeps growing bigger and bigger without ever settling on a single number, or if it jumps around without a clear pattern, then it's called a divergent series. It's like trying to reach a finish line that keeps moving further away!
Contents
What is a Divergent Series?
A divergent series is an infinite series that doesn't have a specific, finite total. Think of it as an endless sum of numbers that never reaches a fixed value. This is different from a convergent series, where the sum of its infinite terms gets closer and closer to a single, definite number.
Understanding Infinite Series
An infinite series is simply a list of numbers that goes on forever, and you're trying to add them all up. For example, you could have:
- 1 + 2 + 3 + 4 + ...
- 1/2 + 1/4 + 1/8 + 1/16 + ...
To understand if a series converges or diverges, mathematicians look at something called "partial sums." A partial sum is what you get when you add up only the first few terms of the series.
- For 1 + 2 + 3 + 4 + ..., the first partial sum is 1. The second is 1+2=3. The third is 1+2+3=6, and so on.
- For 1/2 + 1/4 + 1/8 + ..., the first partial sum is 1/2. The second is 1/2+1/4=3/4. The third is 1/2+1/4+1/8=7/8.
If these partial sums get closer and closer to a specific number as you add more and more terms, the series is convergent. If they don't, it's divergent.
When Does a Series Diverge?
There are a couple of main reasons why an infinite series might diverge:
Terms Don't Approach Zero
If the individual numbers you are adding up don't get closer and closer to zero, then the series will definitely diverge. For example, in the series 1 + 2 + 3 + 4 + ..., the numbers (1, 2, 3, 4, ...) are getting bigger, not smaller. So, when you add them up, the total just keeps growing infinitely.
Terms Approach Zero, But the Sum Still Grows
This is a trickier case! Sometimes, the individual numbers you are adding do get smaller and smaller, even approaching zero, but the total sum still doesn't settle on a finite number. It keeps growing, just very slowly.
The Famous Harmonic Series
A great example of this second type of divergence is the harmonic series. It looks like this: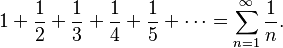 
Here, the numbers you're adding (1, 1/2, 1/3, 1/4, and so on) clearly get smaller and smaller. They even get very close to zero! However, if you keep adding them up, the total sum will slowly but surely grow without any limit. It will eventually pass any number you can imagine, no matter how big.
The fact that the harmonic series diverges was first proven by a smart medieval mathematician named Nicole Oresme. This was a big discovery because it showed that just because the terms get small, it doesn't always mean the sum will be finite.
