Euclidean algorithm facts for kids

The Euclidean algorithm is a clever method used in mathematics. It helps us find the biggest number that can divide two other numbers exactly, without leaving a remainder. This special number is called the greatest common divisor (GCD). It's like finding the largest piece you can cut from two different lengths of string so that both original strings can be made up of only those pieces.

What is the Greatest Common Divisor (GCD)?

The greatest common divisor (GCD) of two numbers is the largest number that divides both of them without any remainder. For example, the numbers 12 and 18 can both be divided by 1, 2, 3, and 6. The largest of these common divisors is 6, so the GCD of 12 and 18 is 6. The Euclidean algorithm is a quick way to find this number, even for very large numbers.

How did Euclid explain it?

The ancient Greek mathematician Euclid probably didn't invent this algorithm, but he wrote about it around 300 BC. He explained it using lengths, not numbers. Imagine you have two lines of different lengths. Euclid's idea was:

If you have two distances, AB and CD, and you always take away the smaller from the bigger, you will end up with a distance that measures both of them.

This means you keep subtracting the smaller length from the larger one until you have a remainder that is smaller than the length you just subtracted. You then repeat the process with this remainder and the previous smaller length. The last length you find that divides everything perfectly is the GCD.

How the Algorithm Works Step-by-Step

The Euclidean algorithm works by repeatedly dividing numbers and looking at the remainders. It's a bit like a game of "remainder tag."

Here are the steps to find the GCD of two positive whole numbers, let's call them m and n:

• Step 1: Make sure m is the larger number. If n is larger than m, simply swap them.
• Step 2: Divide m by n and find the remainder. Let's call this remainder r.

* For example, if m is 49 and n is 21: * 49 divided by 21 is 2 with a remainder of 7. So, r = 7.

• Step 3: Now, the old n becomes the new m.

* In our example, 21 becomes the new m.

• Step 4: The remainder r becomes the new n.

* In our example, 7 becomes the new n.

• Step 5: If the new n is not 0, go back to Step 2 and repeat the process.

* So now we divide 21 by 7. * 21 divided by 7 is 3 with a remainder of 0. So, r = 0.

• Step 6: When n finally becomes 0, the number that m holds at that moment is your greatest common divisor!

* Since our remainder was 0, the last m value (which was 7) is the GCD of 49 and 21.

This method always works and is quite fast, even for very large numbers!

Images for kids

• 

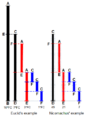
  Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC. The length DC is used to "measure" BA, leaving a remainder EA. Then EA measures DC, leaving FC. Finally, FC measures EA with no remainder. This means FC is the GCD. On the right, an example with numbers 49 and 21, showing their GCD is 7.

• 

  This animation shows the Euclidean algorithm using squares. We start with a rectangle of 1071 by 462. We fit as many 462x462 squares as possible, leaving a smaller rectangle. We repeat this process with the smaller rectangle until no space is left. The side length of the smallest square (21) is the GCD of 1071 and 462.

• 

  The Euclidean algorithm was probably invented before Euclid, who is shown here holding a compass in a painting from around 1474.

• 

  This image shows the distribution of Gaussian primes, which are a special type of number, in a complex number plane. This is related to more advanced number theory.

See also

In Spanish: Algoritmo de Euclides para niños