Five room puzzle facts for kids

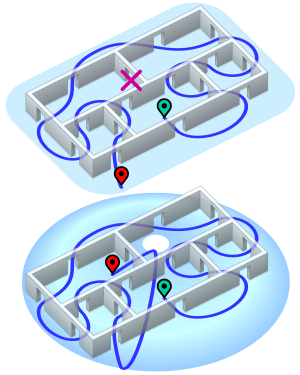
Have you ever heard of the Five-Room Puzzle? It's a famous brain teaser that looks simple but is actually quite tricky! Imagine a big rectangle split into five smaller "rooms." Your goal is to draw a single, continuous line that crosses every "wall" in the diagram, but only once.

Why the Five-Room Puzzle Can't Be Solved

A failed attempt to solve the puzzle on a flat surface. The wall that was missed is shown. Below, a solution on a doughnut shape (torus) is shown. Part of the line goes around the back of the doughnut.

This image compares the graphs of the Seven Bridges of Königsberg (top) and the Five-Room Puzzle (bottom). The numbers show how many lines (edges) connect to each point (vertex). Points with an odd number of lines are orange.

This puzzle is a lot like the famous Seven Bridges of Königsberg puzzle. Both are impossible to solve on a flat surface!

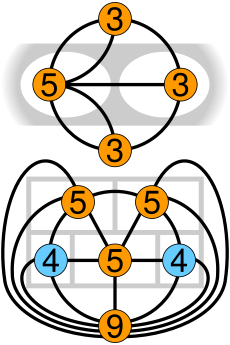
Mathematicians can turn these puzzles into a special kind of map called a graph.

• Each "room" (including the area outside the puzzle) becomes a vertex (a point or dot).
• Each "wall" between rooms becomes an edge (a line connecting the dots).

To solve a puzzle like this, you need to find an Eulerian path. This is a path that crosses every "edge" exactly once. For a path like this to exist, a graph can only have zero or two "vertices" (rooms) with an odd number of "edges" (walls) connected to them.

In the Five-Room Puzzle, if you count the walls for each room (and the outside area), you'll find more than two rooms with an odd number of walls. Because of this, it's impossible to draw a line that crosses every wall exactly once on a flat piece of paper.

However, you could solve a similar puzzle if you change the rules a bit. For example, you could solve it if you were allowed to pass through a corner where two walls meet. Another way to solve it is if you could draw the puzzle on a torus, which is a doughnut shape, instead of a flat surface.

Why It's Impossible: A Simple Explanation

Even without using complicated math terms like "graph theory," we can show why the Five-Room Puzzle has no solution.

Understanding the Rules

First, let's make sure we understand the rules clearly:

• The rooms and your line must all be drawn on one side of a flat piece of paper.
• Your line must be continuous, meaning you can't lift your pencil.
• The line can bend or cross over itself, but it can't cross two walls at the same time (like going through a corner).
• You must cross each "wall" exactly once. "Crossing" means going completely from one room to another, or from a room to the outside area.
• There are 16 walls in total: seven walls separate the rooms from each other, and nine walls separate the rooms from the outside area.

Thinking Like an Observer

We can prove this puzzle is impossible by using a method called proof by contradiction. This means we pretend a solution exists and then show that it leads to something impossible. If it leads to something impossible, then our first idea (that a solution exists) must be wrong.

Imagine there's an "observer" in each of the five rooms. This observer can only see the line when it's inside their room.

• When the line enters a room, the observer sees it come in through one wall.
• When the line leaves a room, the observer sees it go out through another wall.
• The line might also start or end in a room.

What the Observers See

Let's look at the rooms:

• The two rooms at the bottom (lower-left and lower-right) each have four walls.

* If the line starts in one of these rooms, it will leave through one wall, come back through another, leave again, come back through a fourth, and then end. * If the line starts somewhere else, it will enter and leave the room exactly twice, using all four walls. This works fine.

• Now, consider the other three rooms (the top, middle-left, and middle-right rooms). Each of these rooms has five walls.

* If the line starts in one of these rooms, the observer will see it leave (1st wall), then enter and leave again (2nd and 3rd walls), and finally enter and leave a second time (4th and 5th walls). All five walls are crossed. * If the line starts somewhere else, the observer will see it enter and leave (1st and 2nd walls), then enter and leave a second time (3rd and 4th walls). Finally, it will enter through the fifth wall and must end there, because all five walls have been crossed, and the line can't get out again.

So, for any room with five walls, the line must either start inside that room or end inside that room. There's no other way for the line to cross all five walls exactly once.

The Contradiction

We have three rooms that each have five walls. However, any continuous line can only have one starting point and one ending point. This means the line can only start in one of the five-walled rooms and end in another five-walled room. What about the third room with five walls? The line can't start or end there because its start and end points are already used up by the other two five-walled rooms. Since the line cannot start or end in the third five-walled room, it's impossible for it to cross all five of that room's walls.

Because of this, the Five-Room Puzzle cannot be solved according to the rules.