Greedy algorithm facts for kids

Greedy algorithms can help figure out the fewest coins needed to make change. This picture shows how to make 36 cents using coins like 1, 5, 10, and 20 cents. You always pick the largest coin that fits the amount you still need. For many money systems, like the Euro or US Dollar, this simple method works perfectly!

A greedy algorithm is a special kind of algorithm, which is like a set of rules for solving a problem. It works by making the best possible choice at each step, hoping that these small "best" choices will lead to the best overall solution. Think of it as always picking the option that looks most promising right now.

What is a Greedy Algorithm?

A greedy algorithm focuses on finding the best immediate solution. It doesn't look far ahead or consider all possible future outcomes. Instead, it makes a quick decision based on what seems best at that exact moment.

How it Works

Imagine you have a big problem to solve. A greedy algorithm breaks it down into many tiny steps. At each step, it picks the choice that looks best right then. It doesn't worry about whether this choice might cause problems later. It just goes for the immediate "win."

• Local Optimum: This is the best choice you can make at the current step.
• Global Optimum: This is the absolute best solution for the entire problem.

Greedy algorithms hope that picking the local optimum every time will lead to the global optimum.

Examples of Greedy Algorithms

Greedy algorithms are used in many areas of computer science and math. They are often chosen because they are simple and fast.

Finding the Shortest Path

• Dijkstra's algorithm is a famous greedy algorithm. It finds the shortest path between two points in a graph (like a map with roads). It works by always picking the closest unvisited place next.

Connecting Everything with Minimum Cost

• Kruskal's algorithm and Prim's algorithm are also greedy. They help find the cheapest way to connect all parts of a network. Imagine you need to lay cables to connect many houses. These algorithms help you do it with the least amount of cable.

When Greedy Algorithms Don't Work

While greedy algorithms are often very useful, they don't always find the absolute best solution. Sometimes, making the best choice at each step can lead to a bad overall result.

The Coin Problem

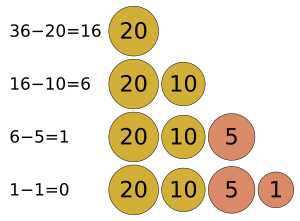
Let's look at the coin-changing example again. Imagine you need to give someone 41 cents in change. You have coins for 25 cents, 10 cents, and 4 cents.

• A greedy algorithm would first pick the largest coin less than 41 cents, which is 25 cents.
• You now need 16 cents (41 - 25 = 16).
• The greedy algorithm picks the largest coin less than 16 cents, which is 10 cents.
• You now need 6 cents (16 - 10 = 6).
• The greedy algorithm picks the largest coin less than 6 cents, which is 4 cents.
• You now need 2 cents (6 - 4 = 2).
• The algorithm gets stuck! You can't make 2 cents with the coins you have.

In this case, the greedy approach failed. A better way to make 41 cents would be:

• One 25-cent coin.
• Four 4-cent coins (4 x 4 = 16 cents).
• Total: 25 + 16 = 41 cents.

This uses 5 coins, while the greedy method got stuck. This shows that sometimes, the "best" choice right now isn't the best for the whole problem.

See also

In Spanish: Algoritmo voraz para niños