Hexacontagon facts for kids
A hexacontagon or 60-gon is a shape that has 60 straight sides and 60 corners. Think of it as a polygon with a lot of sides!
Contents
Regular Hexacontagon
A regular hexacontagon is a special type of hexacontagon. In a regular hexacontagon, all 60 sides are the same length. Also, all 60 angles inside the shape are equal.
You can describe a regular hexacontagon using something called a Schläfli symbol, which for this shape is {60}. This symbol is a quick way to show how many sides a regular polygon has.
A regular hexacontagon can also be made by truncating (which means cutting off the corners of) a triacontagon (a 30-sided shape). If you truncate a triacontagon once, you get a hexacontagon. If you truncate it twice, you get a 120-sided shape!
Angles of a Hexacontagon
In a regular hexacontagon, each inside angle measures 174 degrees. This is very close to a straight line! Because the inside angle is 174 degrees, the outside angle (the angle you'd turn if you walked around the shape) is 6 degrees.
Constructing a Hexacontagon
A regular hexacontagon is a constructible shape. This means you can draw it perfectly using only a compass and a straightedge. This is possible because the number 60 can be broken down into specific prime numbers (60 = 2 x 2 x 3 x 5).
Dissecting a Hexacontagon
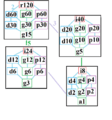
A mathematician named Harold Scott MacDonald Coxeter found that certain polygons can be cut into smaller shapes. A hexacontagon is one of these.
A special type of polygon called a zonogon can be cut into smaller parallelograms. A regular hexacontagon is a zonogon. This means it can be cut into many small diamond-like shapes called rhombi. For a regular hexacontagon, it can be cut into 435 rhombi! Some of these rhombi are actually squares.
Images for kids
-
The symmetries of a regular hexacontagon. This shows how the shape can be rotated or flipped and still look the same.
-
Another way to dissect a 60-gon.
-
A different dissection pattern for a 60-gon.
-
Yet another dissection of a 60-gon.
