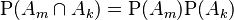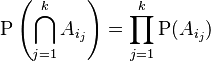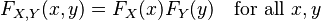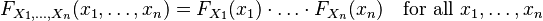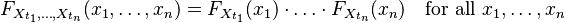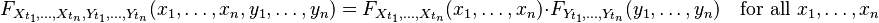kids encyclopedia robot

Independence (probability theory) facts for kids

Kids Encyclopedia Facts


Imagine you have two things that can happen, like flipping a coin and rolling a dice. If what happens with the coin doesn't change the chances of what happens with the dice, then those two things are independent. This idea is super important in understanding probability, which is all about how likely things are to happen.

Sometimes, we talk about things being "statistically independent" or "stochastically independent." It all means the same thing: one event happening doesn't affect the chance of another event happening.

When we have more than two events, like flipping three coins, we need to be careful.

  • Pairwise independent means that any two events from the group are independent of each other.
  • Mutually independent (or collectively independent) means that every event is independent of any combination of the other events. This is a stronger type of independence.

If events are mutually independent, they are also pairwise independent. But being pairwise independent doesn't always mean they are mutually independent. When people just say "independent" in probability, they usually mean mutually independent.

What Does Independence Mean?

For Events

Two Events

Let's say we have two events, Event A and Event B. They are independent if the chance of both A and B happening is the same as multiplying the chance of A happening by the chance of B happening.

\mathrm{P}(A \cap B) = \mathrm{P}(A)\mathrm{P}(B)

 

 

 

 

(Eq.1)

Here, `P(A)` is the probability (or chance) of Event A, and `P(B)` is the probability of Event B. `P(A ∩ B)` means the probability of both A and B happening.

Think of it this way: if you know Event B has happened, does that change the probability of Event A happening? If the answer is no, then they are independent!

  • If A and B are independent, then the probability of A happening, given that B has already happened, is just the probability of A.
  • Also, the probability of B happening, given that A has already happened, is just the probability of B.

This definition is good because it works even if the probability of A or B is zero. It also clearly shows that if A is independent of B, then B is also independent of A.

More Than Two Events

When you have a group of events, like Event A, Event B, and Event C:

  • Pairwise independent means that every pair of events in the group is independent. So, A and B are independent, A and C are independent, and B and C are independent.

\mathrm{P}(A_m \cap A_k) = \mathrm{P}(A_m)\mathrm{P}(A_k)

 

 

 

 

(Eq.2)
  • Mutually independent means that the probability of any combination of these events happening together is the product of their individual probabilities. This is a stronger condition. For example, for three events A, B, and C to be mutually independent, you need:

* P(A ∩ B) = P(A)P(B) * P(A ∩ C) = P(A)P(C) * P(B ∩ C) = P(B)P(C) * AND P(A ∩ B ∩ C) = P(A)P(B)P(C)

\mathrm{P}\left(\bigcap_{j=1}^k A_{i_j} \right)=\prod_{j=1}^k \mathrm{P}(A_{i_j} )

 

 

 

 

(Eq.3)

This is called the multiplication rule for independent events. It must be true for all possible smaller groups of events, not just the whole group at once.

For Random Variables

A random variable is basically a way to assign a number to the outcome of a random event. For example, if you roll a dice, the number you get is a random variable.

Two Random Variables

Two random variables, say X and Y, are independent if knowing the value of one doesn't change the probability distribution of the other.

This means that the chance of X being less than a certain number `x` AND Y being less than a certain number `y` is simply the chance of X being less than `x` multiplied by the chance of Y being less than `y`.

F_{X,Y}(x,y) = F_X(x) F_Y(y) \quad \text{for all } x,y

 

 

 

 

(Eq.4)

If we're talking about probability densities (which are used for continuous random variables), it means:

  • `f_{X,Y}(x,y) = f_X(x) f_Y(y)`

More Than Two Random Variables

Similar to events, a group of random variables is mutually independent if the chance of all of them being less than certain values is the product of their individual chances.

F_{X_1,\ldots,X_n}(x_1,\ldots,x_n) = F_{X_1}(x_1) \cdot \ldots \cdot F_{X_n}(x_n) \quad \text{for all } x_1,\ldots,x_n

 

 

 

 

(Eq.5)

This means that if you have a group of random variables, knowing the values of some of them doesn't give you any extra information about the others.

For Random Vectors

A random vector is just a collection of random variables grouped together. For example, if you measure a person's height and weight, those two measurements could form a random vector.

Two random vectors, say X and Y, are independent if their combined probability distribution is the product of their individual distributions.

F_{\mathbf{X,Y}}(\mathbf{x,y}) = F_{\mathbf{X}}(\mathbf{x}) \cdot F_{\mathbf{Y}}(\mathbf{y}) \quad \text{for all } \mathbf{x},\mathbf{y}

 

 

 

 

(Eq.6)

This means that the information in one random vector doesn't tell you anything about the other random vector.

For Stochastic Processes

A stochastic process is like a sequence of random variables over time. Think of the temperature readings every hour, or the stock price every minute.

Independence Within One Stochastic Process

A single stochastic process is called independent if the random variables at any different points in time are independent of each other.

F_{X_{t_1},\ldots,X_{t_n}}(x_1,\ldots,x_n) = F_{X_{t_1}}(x_1) \cdot \ldots \cdot F_{X_{t_n}}(x_n) \quad \text{for all } x_1,\ldots,x_n

 

 

 

 

(Eq.7)

This means that what happens at one moment in the process doesn't affect what happens at another moment.

Independence Between Two Stochastic Processes

Two different stochastic processes, say X and Y, are independent if their random variables at any given times are independent of each other.

F_{X_{t_1},\ldots,X_{t_n},Y_{t_1},\ldots,Y_{t_n}}(x_1,\ldots,x_n,y_1,\ldots,y_n) = F_{X_{t_1},\ldots,X_{t_n}}(x_1,\ldots,x_n) \cdot F_{Y_{t_1},\ldots,Y_{t_n}}(y_1,\ldots,y_n) \quad \text{for all } x_1,\ldots,x_n

 

 

 

 

(Eq.8)

So, if you have two different processes, knowing what happens in one process doesn't help you predict what happens in the other.

Key Properties of Independence

Self-Independence

An event can only be independent of itself if its probability is either 0 (it never happens) or 1 (it always happens).

  • If `P(A) = 0`, then `P(A ∩ A) = P(A) = 0`. And `P(A) * P(A) = 0 * 0 = 0`. So, `0 = 0`.
  • If `P(A) = 1`, then `P(A ∩ A) = P(A) = 1`. And `P(A) * P(A) = 1 * 1 = 1`. So, `1 = 1`.

Expectation and Covariance

If two random variables, X and Y, are independent, then the average of their product is the product of their averages.

  • `E[XY] = E[X]E[Y]`

Also, their covariance is zero. Covariance measures how much two variables change together. If they are independent, they don't change together, so their covariance is zero.

  • `Cov[X,Y] = E[XY] - E[X]E[Y] = 0`

However, if the covariance is zero, it doesn't automatically mean the variables are independent. They could still be related in a complicated way.

Examples of Independence

Rolling Dice

  • The event of getting a 6 on your first dice roll and the event of getting a 6 on your second dice roll are independent. What you roll the first time doesn't change the chances for the second roll.
  • But, the event of getting a 6 on your first roll and the event that the sum of your two rolls is 8 are not independent. If you get a 6 on the first roll, it changes the possible outcomes for the second roll to make the sum 8 (you'd need a 2).

Drawing Cards

  • If you draw two cards from a deck with replacement (meaning you put the first card back before drawing the second), the event of drawing a red card first and drawing a red card second are independent. The deck is the same for both draws.
  • If you draw two cards without replacement (you keep the first card out), the events are not independent. If you draw a red card first, there are fewer red cards left in the deck, so the chance of drawing another red card changes.

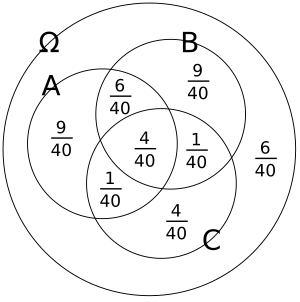
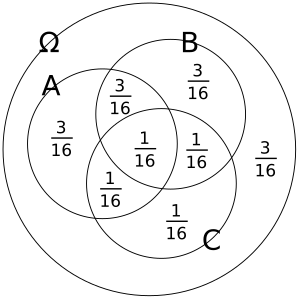
Pairwise vs. Mutual Independence

Pairwise independent
Pairwise independent, but not mutually independent, events
Mutually independent
Mutually independent events

Look at the pictures above. They show different ways events can be independent.

  • In the first picture, the events are pairwise independent. This means if you pick any two events, they don't affect each other. But if you look at all three together, they are not mutually independent.
  • In the second picture, the events are mutually independent. This means any combination of events doesn't affect the others.

To see the difference, imagine you know two events have happened.

  • In the pairwise independent case, knowing two events happened *does* change the probability of the third event.
  • In the mutually independent case, knowing two events happened *does not* change the probability of the third event.

Conditional Independence

For Events

Two events, A and B, are conditionally independent given a third event C if they become independent once you know that C has happened.

  • `P(A ∩ B | C) = P(A | C) * P(B | C)`

This means that if C has occurred, then the chance of A and B both happening is the product of their individual chances, given C.

For Random Variables

Imagine you have two random variables, X and Y. They are conditionally independent given Z if, once you know the value of Z, knowing Y doesn't give you any more information about X.

For example, if you measure the same thing twice (X and Y are your measurements), they might not be independent because they both depend on the actual value (Z). But if you know the actual value Z, then your two measurements X and Y might become independent (unless there's a connection in how you made the errors).

If X and Y are conditionally independent given Z, it means:

  • The probability of X being a certain value, given Y and Z, is the same as the probability of X being that value, given only Z.

Independence is like a special case of conditional independence, where there are no other events or variables to consider.

kids search engine
All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:
Independence (probability theory) Facts for Kids. Kiddle Encyclopedia.