Expected value facts for kids
Imagine you're playing a game or doing an experiment where things happen by chance, like rolling a dice or flipping a coin. The expected value is like predicting the average outcome if you play that game or do that experiment many, many times. It's not what you'll get every single time, but what you'd expect to get on average over the long run.
In probability theory and statistics, the expected value helps us understand what might happen in situations involving randomness. It's a way to figure out the most likely average result.
Contents
What is Expected Value?
The expected value is often called the "long-term average" or "mean" of a random event. It tells you what result to expect if you repeat an experiment many times. It's not a value you'll necessarily get in a single try.
For example, if you flip a fair coin, the chance of getting heads is 50% and tails is 50%. If you assign a value of 1 for heads and 0 for tails, the expected value would be 0.5. You can't flip half a head, but over many flips, your average will get closer to 0.5.
How to Calculate Expected Value
To find the expected value, you multiply each possible outcome by its probability. Then, you add all these results together.
Dice Roll Example
Let's say you roll a standard six-sided dice. The possible outcomes are 1, 2, 3, 4, 5, or 6. Each number has a 1/6 chance of appearing.
- Outcome 1: 1 x (1/6) = 1/6
- Outcome 2: 2 x (1/6) = 2/6
- Outcome 3: 3 x (1/6) = 3/6
- Outcome 4: 4 x (1/6) = 4/6
- Outcome 5: 5 x (1/6) = 5/6
- Outcome 6: 6 x (1/6) = 6/6
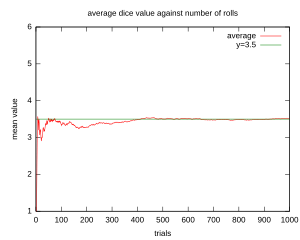
Now, add them all up: 1/6 + 2/6 + 3/6 + 4/6 + 5/6 + 6/6 = 21/6 = 3.5
So, the expected value of rolling a dice is 3.5. You can never roll a 3.5, but if you roll the dice many times, the average of all your rolls will get closer and closer to 3.5.
Coin Flip Example
Imagine a game where you get $1 for heads and lose $1 for tails.
- Probability of heads (H) = 0.5
- Probability of tails (T) = 0.5
Expected Value = (Value of H x Probability of H) + (Value of T x Probability of T) Expected Value = ($1 x 0.5) + (-$1 x 0.5) Expected Value = $0.50 - $0.50 = $0
This means that if you play this game many times, you'd expect to break even on average.
The Law of Large Numbers
The idea that your average results get closer to the expected value over many tries is called the Law of large numbers. It's a very important rule in probability. It basically says that the more times you repeat a random experiment, the closer your average outcome will be to the true expected value.
Why is Expected Value Important?
Expected value is used in many real-world situations, not just games.
- Insurance Companies: They use expected value to set policy prices. They calculate the expected cost of claims for a group of people.
- Gambling and Games: Casinos use expected value to make sure they always have an advantage over players in the long run.
- Business Decisions: Companies use it to decide if a new project is worth investing in. They look at the expected profit or loss.
- Science: Scientists use it to predict outcomes in experiments or studies.
It helps us make smart decisions when dealing with uncertainty.
Related Ideas
- Standard deviation: This measures how spread out the possible outcomes are from the average.
- Variance: This is another measure of how much the results might vary.
See also
 In Spanish: Esperanza (matemática) para niños
In Spanish: Esperanza (matemática) para niños