Random variable facts for kids
A random variable is a special idea in mathematics that helps us understand probability. It's like a rule that turns the results of a chance event into numbers or other simple outcomes. We use random variables to figure out the chances of things happening in real life, like rolling a dice or picking a card.
Contents
What is a Random Variable?
Imagine you have a set of all possible things that can happen in an experiment. This is called the sample space. A random variable is a way to connect each of these possible outcomes to a number or a specific category.
For example, if you flip a coin, the possible outcomes are heads or tails. A random variable could turn "heads" into the number 1 and "tails" into the number 0. Or, if you roll a dice, the outcomes are 1, 2, 3, 4, 5, or 6. A random variable could be the number you roll.
Random variables are usually shown with capital letters like X, Y, or Z. They can be:
- Discrete: This means they can only take on specific, separate values (like whole numbers: 0, 1, 2, 3...).
- Continuous: This means they can take on any value within a range (like height, which can be 150 cm, 150.5 cm, 150.55 cm, and so on).
How Random Variables Help with Probability
Random variables help us link the chance of something happening to a specific value or outcome. When we talk about the probability of an event, we are often talking about the probability that a random variable will take on a certain value or fall within a certain range.
For example, if our random variable X represents the number rolled on a dice, then the probability that X is equal to 3 (written as P(X=3)) is 1/6, because there's one chance out of six to roll a 3.
Dice Examples: Understanding Random Variables
Let's look at some examples using a dice to make this clearer. When you roll a dice, there are 6 possible things that can happen: you can roll a 1, 2, 3, 4, 5, or 6.
Dicing Fruit: A Fair Dice
Here's an example of how a random variable works. Imagine you roll a fair dice once.
- If the number you roll is an odd number (1, 3, or 5), you eat an apple.
- If the number is an even number (2, 4, or 6), you eat an orange.
The random variable here is the type of fruit you will eat. Before you roll the dice, you don't know if you will eat an apple or an orange.
Let's use some math ideas:
- The sample space (all possible dice rolls) is {1, 2, 3, 4, 5, 6}.
- The outcomes for our random variable are {apple, orange}.
We can write our random variable, let's call it X, like this:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): X(\omega)= \begin{cases} apple & \text{ if } \omega \text{ is odd}; \\ orange & \text{ if } \omega \text{ is even}. \end{cases}
Here,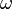 
stands for the number you roll on the dice. Since the dice is fair, the chance of rolling any single number (1, 2, 3, 4, 5, or 6) is 1 out of 6.
The event that you eat an apple happens if you roll a 1, 3, or 5. So, the probability of eating an apple is the chance of rolling a 1, plus the chance of rolling a 3, plus the chance of rolling a 5. This is 1/6 + 1/6 + 1/6 = 3/6 = 1/2. So, you have a 1/2 chance of eating an apple.
Dicing Fruit: An Unfair Dice
Now, let's try the same experiment but with an unbalanced dice. This means some numbers are more likely to be rolled than others.
For example, imagine a dice that has been changed so it never rolls the number 5. The random variable is exactly the same as before:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): X(\omega)= \begin{cases} apple & \text{ if } \omega \text{ is odd}; \\ orange & \text{ if } \omega \text{ is even}. \end{cases}
The possible outcomes (apple or orange) haven't changed. What has changed is the probability of eating an apple or an orange.
With this unfair dice, the chances of rolling numbers are different:
- The chance of rolling 1, 2, 3, 4, or 6 is 1 out of 5 (since 5 is impossible, there are only 5 possible outcomes left).
- The chance of rolling a 5 is 0.
The event that you eat an apple is still when you roll a 1, 3, or 5. But now, the probability is different:
- Chance of rolling 1: 1/5
- Chance of rolling 3: 1/5
- Chance of rolling 5: 0
So, the probability of eating an apple is 1/5 + 1/5 + 0 = 2/5. This is less than the 1/2 chance we had with the fair dice, because rolling a 5 (which would have given you an apple) is now impossible.
Probability Spaces
As you can see from the examples, the same random variable can lead to different probabilities if the chances of the original events change. To avoid confusion, mathematicians often define a random variable as part of a probability space. This space includes the sample space, the event space, and the specific way probabilities are measured. This makes sure everyone knows exactly what probabilities are being talked about.
Related pages
See also
In Spanish: Variable aleatoria para niños
